Transversaler
En rät linje som skär två sidor i en triangel kallas en transversal. Om en transversal dessutom är parallell med triangelns tredje sida kallas den för en parallelltransversal.
Med hjälp av begreppet parallelltransversal kan vi formulera de två geometriska satser som vi ska gå igenom i detta avsnitt: topptriangelsatsen och transversalsatsen.
I bilden nedan är linjen DE en parallelltransversal till triangeln ABC. ADE bildar tillsammans en så kallad topptriangel.
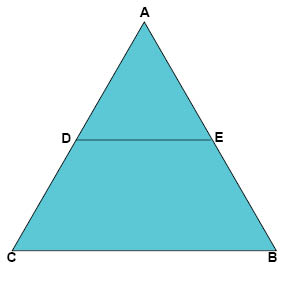
Topptriangelsatsen
Topptriangelsatsen talar om för oss att den topptriangel (ADE i figuren nedan) som bildas av en parallelltransversal är likformig med hela triangeln (ABC i figuren nedan).
$$\bigtriangleup ADE\sim \bigtriangleup ABC$$

Bevis
För att bevisa topptriangelsatsen måste vi visa att trianglarna ADE och ABC är likformiga. Av definitionen av likformighet följer det att om två vinklar i trianglarna ADE och ABC är lika stora, så är trianglarna likformiga.
Kan vi därför visa att två av vinklarna i ADE och ABC är lika stora, då har vi alltså visat att trianglarna är likformiga och således att topptriangelsatsen gäller.
Vinkeln A är gemensam för de båda trianglarna, vilket gör att
$$\measuredangle DAE=\measuredangle CAB$$
Vidare tittar vi vidare på vinkelarna \(\measuredangle\)AED och \(\measuredangle\)ABC och undersöker om de är lika stora. Vi börjar först med att förklara likbelägna vinklar:
Likbelägna vinklar: När en transversal skär två linjer kallas vinklarna som är på samma sida av transversalen och linjerna som transversalen skär igenom för likbelägna vinklar. Alltså vinklar som har ett motsvarande läge i de båda skärningspunkterna. Vidare följer det att om linjerna som transversalen skär igenom är parallella är de likbelägna vinklarna lika stora.
Vi återgår till beviset. Vi vet att i triangeln ABC är linjen DE parallell med sidan CB. Vidare vet vi att \(\measuredangle\)AED och \(\measuredangle\)ABC är likbelägna vinklar vid parallella linjer. Från detta följer det att:
$$\measuredangle AED=\measuredangle ABC$$
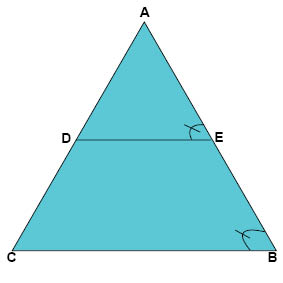
Eftersom två av vinklarna i trianglarna ADE och ABC är lika stora, så innebär det att alla motsvarande vinklarna i trianglarna är lika stora och därför är trianglarna likformiga.
$$\bigtriangleup ADE\sim \bigtriangleup ABC$$
V.S.B.
Transversalsatsen
Transversalsatsen säger att en parallelltransversal som delar två sidor av en triangel, delar dessa båda sidor i samma förhållande, vilket gör att
$$\frac{a}{b}=\frac{c}{d}\text{ eller } \frac{b}{a}=\frac{d}{c}$$
om vi använder beteckningarna för trianglarnas sidor enligt figuren nedan.
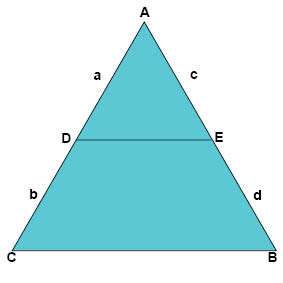
Bevis
Från beviset av topptriangelsatsen här ovanför så vet vi att vinklarna \(\measuredangle\)AED och \(\measuredangle\)ABC är lika stora samt att vinklarna \(\measuredangle\)ADE och \(\measuredangle\)ACB är lika stora eftersom den hela triangeln och topptriangeln är likformiga.
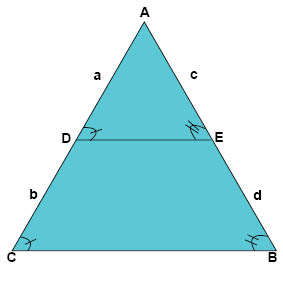
Eftersom trianglarna är likformiga så är förhållandet mellan sidorna lika stort det vill säga
$$\frac{a+b}{a}=\frac{c+d}{c}$$
Vi förenklar uttrycket genom att multiplicera båda leden med ac:
$$\frac{ac\cdot (a+b) }{a}=\frac{ac\cdot (c+d )}{c}$$
$$c\cdot(a+b)=a\cdot(c+d)$$
Härifrån kan vi sedan fortsätta förenkla uttrycket genom att multiplicera in c respektive a i parenteserna:
$$c\cdot(a+b)=a\cdot(c+d)$$
$${\color{Red} \not}{ac}+ bc={\color{Red} \not}{ac}+ad$$
$$bc=ad$$
$$\frac{a}{b}=\frac{c}{d}$$
Detta är den första delen av satsen. Den andra delen får vi genom att skriva om detta samband:
$$\frac{a}{b}=\frac{c}{d}$$
$$\frac{a\cdot {\color{Blue} {b\cdot d}}}{b}=\frac{{\color{Blue} b}\cdot c\cdot {\color{Blue} d}}{d} \Rightarrow$$
$$a\cdot d=b\cdot c$$
$$\frac{a\cdot d}{{\color{Blue} {a\cdot c}}}=\frac{b\cdot c}{{\color{Blue} {a\cdot c}}} \Rightarrow$$
$$\frac{d}{c}=\frac{b}{a}$$
V.S.B
Vi avslutar detta avsnitt med ett exempel där vi kan lösa en uppgift med både topptriangelsatsen och transversalsatsen.
I triangeln \( \bigtriangleup ABC \) är sträckan \(DE\) parallell med \(AB\) Beräkna sträckan \(CE\) som vi markerat med \(x\)

Lösning med topptriangelsatsen:
Tack vare topptriangelsatsen vet vi att trianglarna är likformiga och då kan vi ställa upp och lösa följande ekvation
$$\frac{AC}{CD} = \frac{BC}{CE}$$
$$\frac{38}{18} = \frac{10+x}{x}$$
För att bli av med nämnaren i båda leden multiplicerar vi båda sidor av ekvationen med \(18x\)
$$\frac{18x\cdot 38}{18} = \frac{18x(10+x)}{x}$$
$$38x = 18(10+x) $$
$$38x = 180 +18x$$
$$20x = 180$$
$$x = 9$$
Svar sträckan \(CE\) är 9 cm lång.
Vi fick ut ett svar, men vi testar ändå att lösa uppgiften på ett annat sätt.
Lösning med transversalsatsen:
Med hjälp av transversalsatsen så kan vi ställa upp och lösa följande ekvation
$$\frac{CE}{BE} = \frac{CD}{AD}$$
$$\frac{x}{10} = \frac{18}{20}$$
$$\frac{10\cdot x}{10} = \frac{10\cdot 18}{20}$$
$$x = \frac{180}{20}$$
$$x = 9$$
Även här fick vi att sträckan \(CE\) är 9 cm lång.
Här går vi igenom begreppen sidovinklar, vertikalvinklar, alternatvinklar och likbelägna vinklar.
Här går vi igenom transversalsatsen.
Här går vi igenom beviset för transversalsatsen.
Exempel med topptriangelsatsen.
Fler exempel med topptriangelsatsen.
- Transversal: en rät linje som skär två sidor i en triangel
- Parallella linjer: linjer som har samma lutning och därför har samma avstånd till varandra utan att någonsin skära varandra.
- Parallelltransversal: en transversal som är parallell med en sida i en triangel
- Likformighet: om två trianglar ärlikformiga betyder att de har exakt samma form, men inte nödvändigtvis samma storlek
- Topptriangel: en mindre triangel i en annan triangel som skapas av en transversal
- Topptriangelsatsen: Topptriangelsatsen talar om för oss att den topptriangel som bildas av enparallelltransversal är likformig med hela triangeln
- Transversalsatsen: en parallelltransversal som delar två sidor av en triangel, delar dessa båda sidor i samma förhållande,
$$\frac{a}{b}=\frac{c}{d}\text{ eller } \frac{b}{a}=\frac{d}{c}$$
om vi använder beteckningarna för trianglarnas sidor enligt figuren nedan.

- Likbelägna vinklar:

I bilden så är linjerna A och B parallella. Om två linjer A och B är parallella så skriver vi det på följande sätt \( A \parallel B\). Alltså är \(\varepsilon\) och \(\eta\) är likbelägna vinklar och därför lika stora.
