Exponentialfunktioner

Vi har tidigare i Matte 2-kursen tittat på linjära funktioner och andragradsfunktioner, där vi har haft den oberoende variabeln x i basen av en potens.

En funktion där den oberoende variabeln, vanligen betecknad x, återfinns i exponenten till en potens kallas för en exponentialfunktion.

En exponentialfunktion skrivs på den allmänna formen:

$$f(x) = C \cdot a^{x}$$

där C och a är konstanter (a > 0), x är den oberoende variabeln och y är den beroende variabeln. Som vi ser finns alltså den oberoende variabeln, x, i exponenten, medan potensens bas utgörs av en konstant, a.

Värdet på basen a i en exponentialfunktion

En exponentialfunktion ser olika ut beroende på om basen a är större eller mindre än 1 (basen a är dock alltid större än 0).

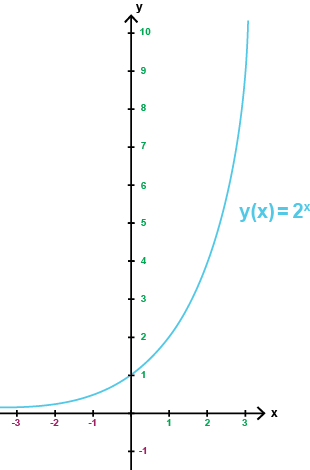
I koordinatsystemet nedan har vi skissat in grafen till exponentialfunktionen

$$f(x)=2^x$$

I denna funktion är basen större än 1 (a = 2)

Funktionen är då växande för alla värden på x.

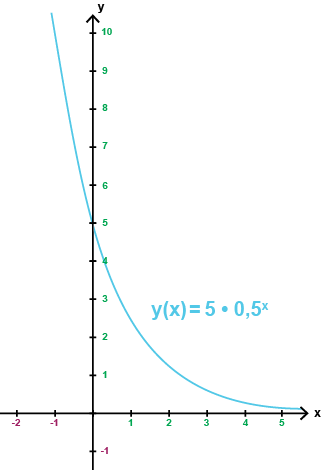
Nedan har vi i ett koordinatsystem skissat upp grafen till exponentialfunktionen

$$f(x)=5\cdot 0,5^x$$

Denna funktion har en bas som är mindre än 1 (a = 0,5). Funktionen är då avtagande för alla värden på x. Ju större värde x antar, desto närmare f(x) = 0 kommer funktionsvärdet att komma, men det kommer aldrig att nå ända ner till f(x) = 0.

Med hjälp av potensregeln för negativa exponenter

$$a^{-x} = \frac{1}{a^{x}}$$

kan vi skriva om exponentialfunktioner där basen a är mindre än 1 för att få fram exponentialfunktioner med en negativ exponent (eller tvärtom).

Om vi använder oss av detta samband kan vi skriva om funktionen i exemplet ovan på följande sätt:

$$f(x)=5\cdot 0,5^x$$

$$f(x)=5\cdot \left ( \frac{1}{2} \right )^x$$

$$f(x)=5\cdot \, \frac{1}{2^x}$$

$$f(x)=5\cdot 2^{-x}$$

Med andra ord är funktion \( f(x) = 5 \cdot 0,5^x\) densamma som \(f(x) = 5 \cdot 2^{-x}\).

Värdet på koefficienten C i en exponentialfunktion

Precis som kurvans utseende påverkades av storleken på basen a så påverkas kurvans utseende av värdet av koefficienten C.

Koefficienten C kan vi tolka som det funktionsvärde som funktionen har då x = 0, det vill säga var kurvan skär y-axeln. Sätter vi in x = 0 i en exponentialfunktion med basen a, så får vi ju

$$f(0)=C\cdot a^0=C\cdot 1=C$$

Grafisk lösning av exponentialfunktioner

Ett exempel på en exponentialfunktion kan vi se här nedanför

$$f(x)=50000\cdot 1,02^x$$

Funktionen beskriver hur mycket pengar (f(x)) vi har på ett bankkonto om vi sätter in 50 000 kronor på ett konto med en årlig ränta på 2 % (förändringsfaktor 1,02), där x är antalet år efter att vi satte in pengarna.

Om vi vill veta hur mycket pengar vi har på kontot efter 3 år behöver vi bara sätta in 3 istället för x och räkna ut vad vi då får för funktionsvärde:

$$f(3)=50000\cdot 1,02^3 = 53060,40$$

Med andra ord så kommer vi ha 53 060,40 kronor på kontot efter 3 år.

Om vi istället vill ta reda på hur många år det tar tills vi har sparat ihop till 60 000 kronor på kontot, så kan vi lösa detta grafiskt. Den metod som vi kommer att använda här är i grunden samma metod som vi i Matte 1-kursen använde för grafisk lösning av ekvationer.

Vi beskriver den önskade situationen som en exponentialekvation, där vårt valda funktionsvärde alltså ska vara 60 000 (60 000 kr ska finnas på kontot)

$$50000 \cdot 1,02^{x} = 60000$$

För att lösa denna ekvation grafiskt ritar vi in följande funktioner i ett koordinatsystem

$$f(x)=50000\cdot 1,02^x$$

$$f(x)=60000$$

och hittar x-koordinaten till skärningspunkten mellan de båda graferna. Denna x-koordinat utgör den sökta lösningen på vår exponentialekvation.

Vi ser att de båda kurvorna skär varandra där x ≈ 9,2, vilket innebär att efter 9,2 år så har vi 60 000 kronor på kontot.

Vad vi gjorde här var alltså att vi löste en exponentialekvation grafiskt. På samma sätt som vi tidigare har sett för till exempel andragradsekvationer, så finns det även sätt att lösa en exponentialekvation algebraiskt, vilket vi ska titta närmare på i de kommande avsnitten.