Likformighet och kongruens

I detta avsnitt kommer vi att gå igenom de båda besläktade begreppen likformighet och kongruens. Dessa begrepp används för att fastställa vissa egenskaper hos geometriska figurer, så som vinklar och längder.

Likformighet

Att två trianglar är likformiga betyder att de har exakt samma form, men inte nödvändigtvis samma storlek.

Vi kan dra slutsatsen att två trianglar är likformiga om två vinklar i den ena triangeln är lika stora som två vinklar i den andra triangeln, och/eller om förhållandet mellan motsvarande sidor i trianglarna är detsamma.

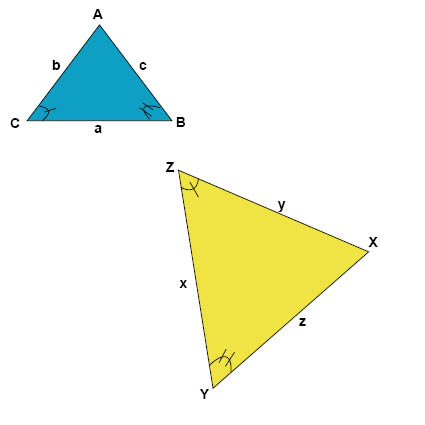
I trianglarna ΔABC och ΔXYZ är två vinklar lika stora. Eftersom vinkelsumman i en triangel alltid är 180° så innebär det att om två vinklar är lika stora i de två trianglarna, så är även den tredje vinkeln lika stor i de båda trianglarna. Därför räcker det med att vi visar att två vinklar är lika stora i den ena triangeln som i den andra för att vi ska veta att de båda trianglarna är likformiga.

Vi betecknar att två trianglar ΔABC och ΔXYZ är likformiga på följande sätt:

$$\bigtriangleup ABC\sim \bigtriangleup XYZ$$

I två likformiga trianglar är förhållandet mellan motsvarande sidor i de båda trianglarna lika, vilket för trianglarna här ovanför betyder att

$$\frac{a}{x}=\frac{b}{y}=\frac{c}{z}$$

Vi tittar på ett exempel. Här nedan har vi två likformiga trianglar. Hitta längden på sidan markerad med \(j\).

Eftersom trianglarna är likformiga så kan vi använda oss av att sidorna kommer ha samma förhållande. Längderna på basen i trianglarna kommer förhålla sig till varandra så som höjderna gör, därför kan vi ställa upp och lösa följande ekvation

$$\frac{j}{2}= \frac{6}{4}$$

$$\frac{j}{2} = \frac{3}{2} $$

$$\frac{2\cdot j}{2} = \frac{3 \cdot 2}{2} $$

$$j = 3$$

Svaret blir att sidan markerad med \(j\) är 3 längdenheter lång.

Alla månghörningar kan vara likformiga. För att två månghörningar ska vara likformiga så måste motsvarande vinklar vara lika stora och förhållandet mellan motsvarande sidor lika stora.

Likformighet är en egenskap som används för att kunna bevisa de satser som vi kommer att ta upp i följande avsnitt: topptriangelsatsen, transversalsatsen och bisektrissatsen.

Kongruens

Två månghörningar är kongruenta om motsvarande vinklar och motsvarande sidor är lika stora. Definitionen av kongruens innebär att alla kongruenta figurer också är likformiga.

Man betecknar att två trianglar ΔABC och ΔDEF är kongruenta på följande sätt:

$$\bigtriangleup ABC\cong \bigtriangleup DEF$$

Två trianglar är kongruenta om ett av följande tre kongruensfall uppfylls (är ett av fallen uppfyllda är de två andra fallen per definition också uppfyllda):

1. Två sidor och den mellanliggande vinkeln är lika stora i de båda trianglarna.
   
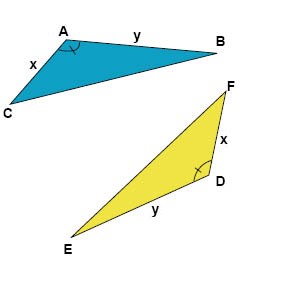
2. Alla tre motsvarande sidor är lika långa i de båda trianglarna.
   
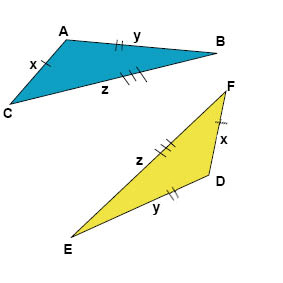
3. Två vinklar och den mellanliggande sidan är lika stora i de båda trianglarna.
   

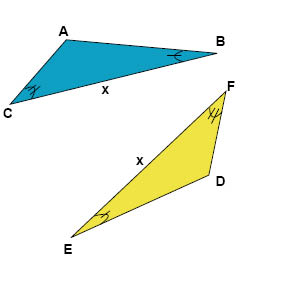
Vi avslutar med ett exempel. Avgör om dessa två trianglar är kongruenta. 

Vi har bara en sida given, men två vinklar som inte är samma eller på varsin sida om sidan, men eftersom vi har två vinklar i varje triangel räcker det för att räkna ut den tredje då vinkelsumman alltid blir \(180^{\circ}\). I den övre triangeln (blå) kan vi beräkna den tredje vinkeln

$$ 180^{\circ}-56,6^{\circ}-42,4^{\circ} = 81^{\circ} $$

Detta överrensstämmer med den undre triangeln (lila) och vi får det tredje kongruensfallet, där vi har två vinklar och den mellanliggande sidan som är lika stora, alltså kan vi säga att trianglarna är kongruenta.