Derivata

Som vi kom fram till i det föregående avsnittet, är en tangent en linje som sammanfaller med kurvan endast i en punkt och i denna punkt har samma lutning som kurvan. När vi låter två punkter på kurvan närma sig varandra alltmer, så kommer sekantens lutning att närma sig tangentens lutning. När vi låter avståndet mellan punkterna gå mot noll kommer sekanten att övergå i tangenten. Det gränsvärde av ändringskvoten (sekantens/tangentens lutning) som vi då kan beräkna kallas för funktionens derivata i den punkten.

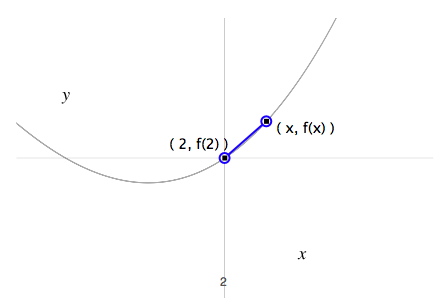
Vi har tidigare i kursen träffat på gränsvärden, men den gången handlade det om att hitta gränsvärden gällande funktionsvärden då en variabel närmar sig ett visst värde. Denna gång använder vi oss av beräkning av ett gränsvärde för att hitta tangentens lutning i en punkt. Nedan är ett exempel på en kurva med en tangent i en punkt.

När vi vill uttrycka gränsvärdet för lutningen i punkten (b), som ligger i (2, 3), så skriver vi

$$k= \lim_{x \to 2 } \frac{f(x)-f(2)}{x-2}$$

lim står för det latinska ordet "limes" som betyder "gräns". Vi kan alltså säga att detta uttryck hör ihop med k-värdet för sista figuren i det förra avsnittet (tangentens lutning), medan uttrycket

$$k= \frac{f(x)-f(2)}{x-2}$$

hör ihop med sekantens lutning:

Det finns ett kortare sätt att beskriva gränsvärdet för (b).

$$k= \lim_{x \to 2 } \frac{f(x)-f(2)}{x-2}=f'(2)$$

f '(2) uttalas "f prim av 2" eller "derivatan då x=2".

Nu ska vi titta på ett exempel där vi beräknar derivata i en punkt utifrån en känd funktion

Funktionen och dess graf har vi här.

$$f(x)=x^{2}+2x$$

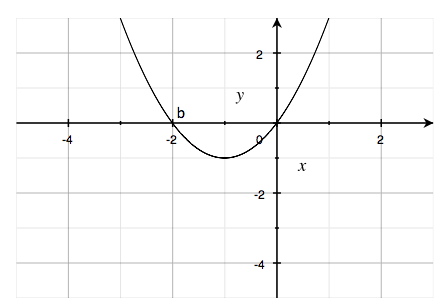
Nu ska vi räkna ut derivata i punkten (b) (det vill säga i den punkt på kurvan där x = -2):

Formeln för detta gränsvärde är:

$$ k=f'(-2)= \lim_{x \to -2 } \frac{f(x)-f(-2)}{x-(-2)}$$

Vi kan inte utan vidare sätta in x=-2 i denna formel, för det skulle ju innebära att vi försöker beräkna en lutning mellan (b) och (b). Vi kan naturligtvis inte använda samma punkt två gånger i formeln för k-värde. Om vi ändå försöker detta ser vi att nämnaren blir lika med noll och kvoten blir odefinierad.

För att beräkna gränsvärdet måste vi faktorisera uttrycket och förkorta det. Vi börjar med att beräkna f(-2).

f(-2) beräknas:

$$f(-2)=(-2)^{2}+2(-2)=4-4=0$$

f '(-2) blir därmed:

$$f'(-2)=\lim_{x\rightarrow -2}\frac{f(x)}{x-(-2)}=\lim_{x\rightarrow -2}\frac{x^{2}+2x}{x+2}=$$

$$=\lim_{x\rightarrow -2}\frac{x\cdot (x+2)}{x+2}=\lim_{x\rightarrow -2}x=-2$$

Den sökta lutningen i punkten på kurvan där x=-2, är alltså f '(-2)=-2.

Så vad är nu skillnaden på f(x) och f '(x) i praktiken? Följande graf visar hur ett föremål stiger upp i luften:

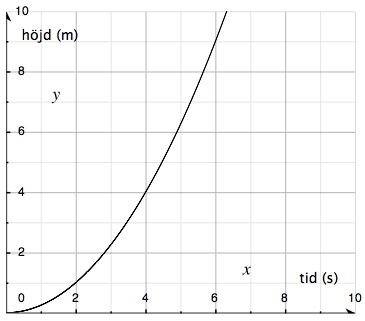
Om vi studerar punkten (2,1):

f(2) är föremålets höjd vid tiden x=2.

f '(2) är föremålets höjdändring vid tiden x = 2 (det vill säga föremålets hastighet, hur snabbt höjden förändras, vid just tidpunkten x = 2)