Växande och avtagande funktion
Vi har gått igenom hur vi kan hitta en funktions derivata genom att använda derivatans definition och därigenom funnit ett antal deriveringsregler. Nu ska vi titta närmare på funktioner och deras grafer, och hur dessa förhåller sig till tangentens lutning.
Beroende på hur tangenten till en kurva lutar, kommer den ha olika k-värden.
Låt oss undersöka den enkla andragradsfunktionen f(x)=x2+1 och dess graf
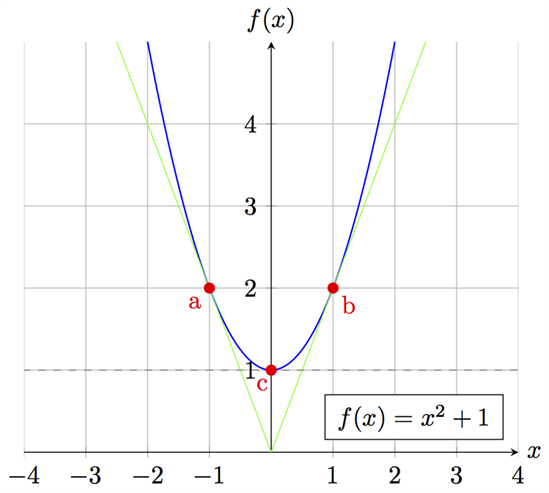
I figuren ovan är tre punkter på kurvan markerade: a med koordinaterna (-1, 2), b med koordinaterna (1, 2), och c med koordinaterna (0, 1).
Punkten a har en tangent som är avtagande. Tangentens k-värde/derivatan i punkten är negativ.
| Om f '(x) < 0 är tangenten i x avtagande. |
Vi kan också se i figuren att tangenten för alla punkter längs kurvan vars x-värde ligger i intervallet
$$-\infty <x<0$$
är avtagande, det vill säga har negativ derivata. Detta gäller alltså alla punkter längs kurvan som ligger till vänster om punkten c i figuren.
En funktion är strängt avtagande i ett intervall
$$a\leq x\leq b$$
om det i detta intervall gäller att varje par av x-värden där x1<x2 också har funktionsvärden där f(x1)>f(x2). Vi kan också uttrycka att en funktion är strängt avtagande i ett intervall om
$$ f'(x)<0$$
gäller för alla x-värden i intervallet.
I vårt exempel är funktionen strängt avtagande i intervallet
$$-\infty<x<0$$
eftersom funktionsvärdet f(x) hela tiden minskar ju större värden på x vi väljer.
Punkten b har en tangent som är växande. Tangentens k-värde/derivatan i punkten är positiv.
| Om f '(x) > 0 är tangenten i x växande. |
På ett liknande sätt som vi gjorde nyss kan vi titta på figuren och se att tangenten för alla punkter längs kurvan vars x-värde ligger i intervallet
$$ 0<x<\infty $$
är växande, det vill säga har positiv derivata. Detta gäller alltså alla punkter längs kurvan som ligger till höger om punkten c i figuren.
En funktion är strängt växande i ett intervall
$$ a\leq x\leq b $$
om det i detta intervall gäller att varje par av x-värden där x1<x2 också har funktionsvärden där f(x1)<f(x2). Vi kan också uttrycka att en funktion är strängt växande i ett intervall om
$$f'(x)>0$$
gäller för alla x-värden i intervallet.
I vårt exempel är funktionen strängt växande i intervallet
$$ 0<x<\infty $$
eftersom funktionsvärdet f(x) hela tiden ökar ju större värden på x vi väljer.
Punkten c har en tangent som är helt horisontell (parallell med x-axeln). Tangentens k-värde/derivatan i punkten är lika med 0.
| Om f '(x) = 0 är tangenten i x horisontell, det vill säga saknar lutning. |
Sammanfattning
Vi har en funktion f(x) som är definierad på ett intervall I och punkterna x1 och x2 ligger i intervallet I.
- f(x) är strängt växande på I om x1 < x2 medför att f(x1) < f(x2)
- f(x) är växande på I om x1 < x2 medför att f(x1) ≤ f(x2)
- f(x) är strängt avtagande på I om x1 < x2 medför att f(x1) > f(x2)
- f(x) är avtagande på I om x1 < x2 medför att f(x1) ≥ f(x2)
Alternativt kan vi formulera om detta så här
- Om f '(x) > 0 för alla x i ett intervall I, så är f(x) strängt växande i I.
- Om f '(x) < 0 för alla x i ett intervall I, så är f(x) strängt avtagande i I.
- Om f '(x) = 0 för alla x i ett intervall I, så är f(x) konstant (horisontell) i I.
Här går vi igenom när en funktion är växande eller avtagande.
Här fortsätter vi gå igenom när en funktion är växande eller avtagande.
Förklaring till hur vi tar reda på om en funktion är växande eller avtagande.
- Derivata: En funktion som beskriver förändringshastigheten (lutningen) till en annan funktion
- Tangent: En rät linje som bara nuddar en kurva en gång, vi kan också säga att en linje tangerar en kurva och den bara nuddar i en punkt
- Riktningskoefficient: Koefficient som anger lutningen i en tangent, k-värdet i \(y= kx+m\)
- Stängt växande: En funktion är strängt växande om funktionsvärdena ökar när värdena i definitionsmängden ökar (kan gälla på ett intervall eller hela funktionen) och vi kan också skriva om \(x_1 < x_2\) medför att \(f(x_1) < f(x_2)\), grafen kommer luta uppåt överallt (eller på intervallet). Då kommer derivatan att vara positiv (\(f^{\prime}(x)>0\)).
- Växande: här får funktionsvärdena vara större eller lika med, det vill säga att om \(x_1 < x_2\) medför att \(f(x_1) \leq f(x_2)\), grafen kommer luta uppåt eller vara platt (\(f^{\prime}(x)\geq 0\)).
- Strängt avtagande: Om en funktion är avtagande så sjunker funktionsvärdena medan värdena i definitionsmängden ökar, det vill säga att om \(x_1 < x_2\) medför att \(f(x_1) > f(x_2)\), grafen kommer luta nedåt överallt. Då kommer derivatan att vara negativ (\(f^{\prime}(x)<0\)).
- Avtagande: Likt tidigare får funktionsvärdena sjunka eller vara samma, det vill säga att om \(x_1 < x_2\) medför att \(f(x_1) \geq f(x_2)\), grafen kommer luta nedåt eller vara platt (\(f^{\prime}(x) \leq 0\)).
