Skissa grafer
I det här avsnittet ska vi titta på hur vi kan skissa en graf utifrån en funktion. Här tar vi hjälp av det vi lärt oss om derivatan i de förgående avsnitten. Vi tittar också på det särskilda fallet med andragradsfunktioner där vi kan beräkna extremvärden och extrempunkter utan att använda derivata.
Skissa en graf
I förra avsnittet lärde vi oss om "Några typiska funktioners grafer” och vi kan se att graferna varierar till utseendet beroende på hur hög den högsta potensen i funktionen är och vilket tecken koefficienten framför har. Det är den som “styr” grafens (kurvans) utseende. Med utgångspunkt från en algebraisk funktion ska vi skapa och skissa en graf i ett koordinatsystem. För att göra det är det i de flesta fall nödvändigt att bestämma derivatans nollställen, funktionens nollställen, i vilka intervaller funktionen är avtagande respektive växande, funktionens maximi- och minimivärden, eventuella inflexionspunkter, samt i vilket intervall funktionen är definierad. För det särskilda fallet med andragradsfunktioner finns ett enklare sätt, som vi känner igen från Matte 2 och som vi tittar på i följande exempel
Låt oss börja med att ta hjälp av derivata
$$f(x)=x^{2}-x-2$$
a) I vilka intervall är funktionen växande?
En växande kurva har en derivata som är större än noll. Om vi börjar med att hitta x-värden för de punkter där derivatan är lika med noll, så kan vi därefter använda teckenstudium.
Vi deriverar funktionen och sätter derivatan lika med noll. Genom att lösa den ekvation vi får då hittar vi de sökta x-värdena:
$$f'(x)=2x-1$$
$$0=2x-1$$
$$x=0,5$$
I det här fallet hittade vi bara ett x-värde (x=0,5), vilket betyder att funktionen bara har en punkt där tangenten till kurvan är horisontell (derivatan lika med noll).
Vi vet ännu inte om den funna punkten är en maximi-, minimi-, eller terrasspunkt, eller var i y-led punkten befinner sig.
Dock kan vi börja med att skissa funktionens graf utifrån vad vi vet om denna punkt - vi vet att derivatan i punkten är lika med noll (tangenten är horisontell med x-axeln) och vi vet att x-värdet för punkten är x=0,5:
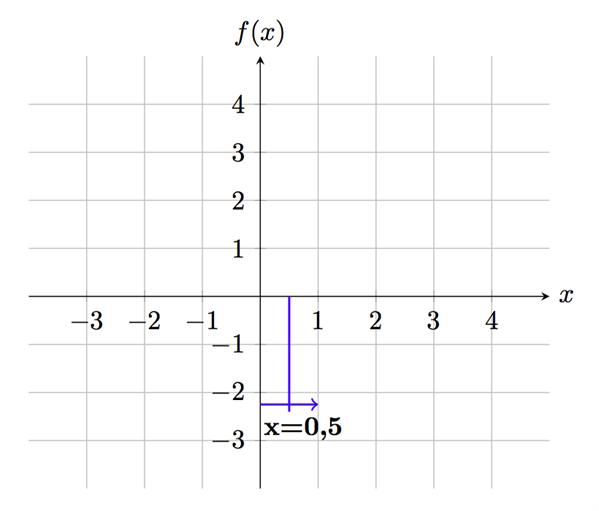
Nu ska vi testa att sätta in ett x-värde större än 0,5 i uttrycket för derivatan, för att se hur lutningen ser ut till höger om punkten. Det kan endast vara en typ av lutning på varje sida (antingen strikt växande eller strikt avtagande), annars hade vi hittat fler punkter tidigare då vi sökte derivatans nollställen:
$$f'(1)=2\cdot 1-1=1$$
Derivatan är positiv i x=1. Kurvan är med andra ord växande till höger om x=0,5. Vi skissar in detta i figuren:
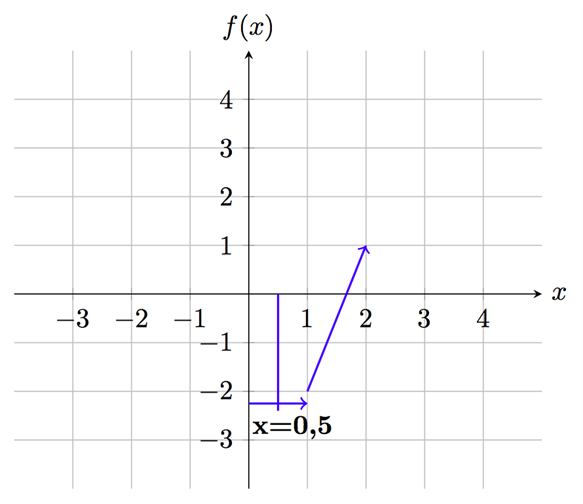
Vi gör likadant med ett x-värde mindre än 0,5 för att se hur derivatan ser ut till vänster om punkten:
$$f'(0)=2\cdot 0-1=-1$$
Derivatan är negativ i x=0. Kurvan är med andra ord avtagande till vänster om x=0,5. Även denna information lägger vi till i figuren, där vi nu börjar ana kurvans form:
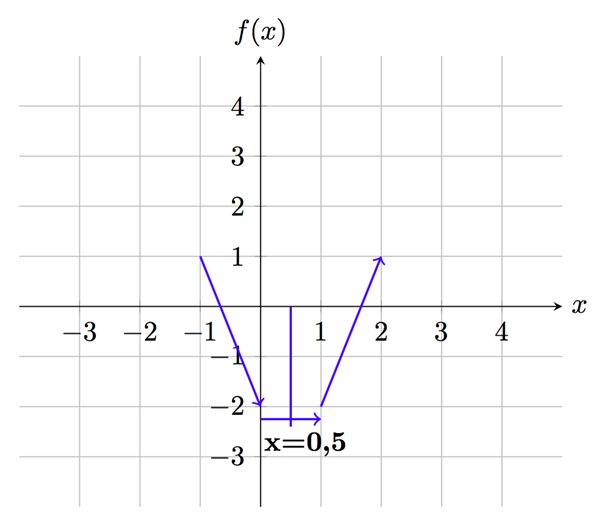
Vi har nu tillräckligt med information för att säga att kurvans liknar en glad mun och har ett minimivärde i x=0,5. För att svara på den inledande frågan i uppgiften kan vi alltså veta att funktionen är växande för x-värden i intervallet
$$x> 0,5$$
vilket ju är för alla punkter på kurvan till höger om minimipunkten.
b) Bestäm kurvans nollställen, samt minimipunktens placering.
Det kan vara lätt att blanda ihop hur vi hittar funktionens nollställen med hur vi hittar möjliga extrempunkters x-värde (där derivatan har ett nollställe). I en möjlig extrempunkt är derivatan 0 (alltså f ´(x)=0); i ett nollställe med avseende på kurvan är funktionsvärdet 0 (alltså f(x)=0, vi befinner oss i detta fall i en punkt någonstans längs x-axeln).
Om vi börjar med att sätta f(x) = 0, så kommer vi alltså att få kurvans nollställen, det vill säga hitta de x-värden där kurvan skär x-axeln. Det gör vi nu:
$$f(x)=x^{2}-x-2$$
$$x^{2}-x-2=0$$
$$x=-\frac{(-1)}{2} \pm\sqrt{\left ( \frac{(-1)}{2} \right )^{2}-(-2)}=$$
$$=\frac{1}{2} \pm\sqrt{\frac{9}{4}}=\frac{1}{2} \pm\frac{3}{2}$$
$$\begin{align} x_{1} & =2 \\ x_{2} & =-1 \end{align}$$
Dessa är alltså de sökta nollställena.
Minimipunktens x-koordinat har vi redan beräknat i a). Allt vi behöver nu är y-koordinaten. Vad gör vi om vi har ett x-värde och vill ha ut ett y-värde? Jo, sätter in x-värdet i f(x):
$$f(0,5)=0,5^{2}-0,5-2=-2,25$$
Nu vet vi minimipunktens koordinater, som alltså är (0,5; -2,25).
Vi sammanfattar denna uppgift genom att skissa grafen till funktionen \(f(x)=x^{2}-x-2\) utifrån den information vi har tagit fram i a) och b):
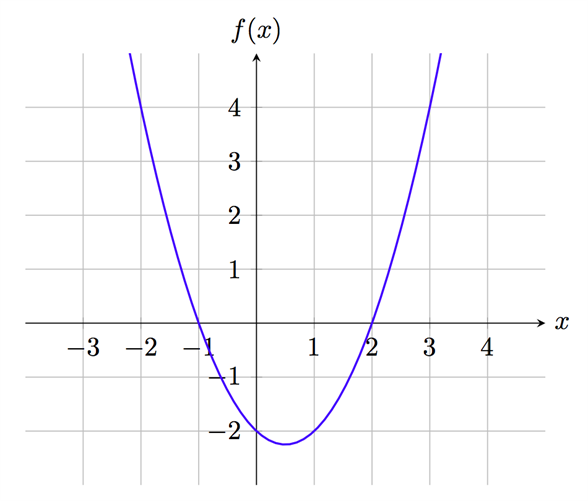
Alternativ metod för andragradsfunktioner:
Låt oss nu göra på ett enklare sätt, nämligen att använda pq-formeln för att skissa en graf.
Det är lämpligt att du har andragradsfunktioner färskt i minnet, följ länken om du vill repetera mer djupgående, men vi tar en kortare repetition nu. Anta att vi har det allmänna uttrycket för en andragradsfunktion
$$f(x) = ax^2 +bx+c = x^2 +px +q$$
Börja med att betrakta koefficienten före den högsta potensen \(x^2\), positiv koefficient framför \(x^2\) innebär att funktionen är en positiv parabel (dvs liknar en “glad mun”), negativ koefficient framför \(x^2\) innebär att funktionen är en negativ parabel (dvs liknar en “sur mun”). Det innebär att om vi har en konvex andragradskurva får vi ett minimivärde i symmetrilinjen och har vi en konkav andragradskurva får vi ett maximivärde i symmetrilinjen. Koefficienten q är det y-värde som funktionen antar där grafen skär y-axeln, alltså när \(x = 0\).
Funktionens nollställen \(f(x) = 0\) kan beräknas med pq-formeln
$$x = - \frac{p}{2} \pm \sqrt{{\left(\frac{p}{2}\right)}^2-q}$$
Vi vet också att en andragradsgraf är symmetrisk kring ett x-värde som är \(-\frac{p}{2}\), vilket framgår av pq-formeln ovan. Observera att om p är ett negativt tal blir \(-\frac{p}{2}\) ett positivt tal. Skillnaden mellan symmetrilinjen \(x = -\frac{p}{2}\) och funktionens båda nollställen är
$$x = \pm \sqrt{{\left(\frac{p}{2}\right)}^2-q}$$
I figuren kan vi avläsa att symmetrilinjen \(x = -\frac{p}{2}\) är identisk med x-värdet för extrempunkten (maximi- eller minimipunkten) och därför blir \(f\left(-\frac{p}{2}\right)\) lika med y-värdet för extrempunkten.
Vi kan också avläsa i figuren att om avståndet mellan symmetrilinjen och nollställena är 0 dvs uttrycket ovan är lika med 0, så har funktionen bara ett nollställe, även kallad dubbelrot. Då tangerar funktionen x-axeln i punkten\(x = -\frac{p}{2}\).
Vidare kan vi konstatera att om nollställen saknas, dvs reella lösningar till pq-formeln ovan saknas, inträffar om uttrycket för nollställen inte har några reella lösningar, då får vi ett negativt tal under rottecknet. Då saknas nollställen.
Nedan har vi en interaktiv bild från GeoGebra där du kan ändra på q-värdet och se hur q-värdet i andragradsfunktonen påverkar nollställena.
Största och minsta värde i ett intervall
Bestäm funktionens största värde i det angivna intervallet:
$$f(x)=x^{4}-2x^{2}$$
$$-1< x\leq 2$$
Vi börjar med att identifiera möjliga extrempunkters x-värden. Det gör vi på samma sätt som tidigare genom att derivera funktionen, sätta derivatan till noll och lösa den resulterande ekvationen:
$$f{}'(x)=4x^{3}-4x$$
$$0=4x\cdot (x^{2}-1)$$
$$x_{1}=0$$
$$x^{2}-1=0 \Rightarrow$$
$$\begin{align} x_{2} & =1 \\ x_{3} & =-1\end{align}$$
Notera att x3=-1 ligger utanför intervallet som vi skulle undersöka. Funktionsvärdet i den möjliga extrempunkt som ligger vid detta x-värde kan därför inte vara del i svaret.
För övrigt har vi två punkter som eventuellt är maximipunkter och därför även är kandidater för att vara det högsta funktionsvärdet i intervallet. Vi har ett möjligt extremvärde som ligger någonstans där x=0 och ett som ligger någonstans där x=1.
Vi beräknar funktionsvärdena (y-värdena) i de tre punkterna, där derivatan alltså är lika med noll:
$$f(-1)=(-1)^{4}-2\cdot (-1)^{2}=1-2=-1\Rightarrow (-1,-1)$$
$$f(0)=0^{4}-2\cdot 0^{2}=0\Rightarrow (0,0)$$
$$f(1)=1^{4}-2\cdot 1^{2}=-1\Rightarrow (1,-1)$$
Vi lägger in dessa tre punkter i en figur. Då får vi en bättre överblick på hur kurvan ser ut:
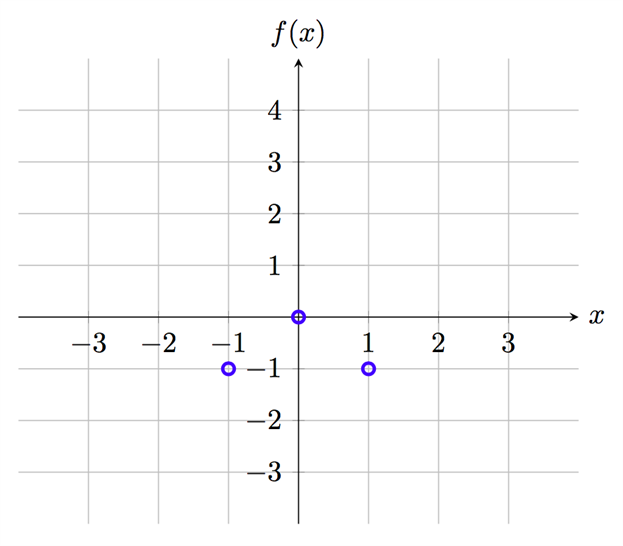
Härefter går vi vidare med teckenstudium. Syftet med teckenstudien är att vi ska ta reda på om var och en av våra punkter är en maximi-, minimi- eller terrasspunkt. För säkerhets skull ska vi identifiera hela kurvan, även den del av kurva som är utanför intervallet.
I uttrycket för funktionens derivata testar vi att sätta in ett värde på x som är mindre än -1, ett x som är större än -1 men mindre än 0, ett x som är större än 0 men mindre än 1, samt ett x som är större än 1:
$$f'(-2)=4\cdot (-2)^{3}-4\cdot (-2)=4\cdot (-8)+8=-24\Rightarrow -$$
$$f'(-0,5)=4\cdot (-0,5)^{3}-4\cdot (-0,5)=4\cdot (-0,125)+2=1,5\Rightarrow +$$
$$f'(0,5)=4\cdot 0,5^{3}-4\cdot 0,5=4\cdot 0,125-2=-1,5\Rightarrow -$$
$$f'(2)=4\cdot 2^{3}-4\cdot 2=4\cdot 8-8=24\Rightarrow +$$
De här resultaten sammanställer vi i en teckentabell:
| x | -2 | -1 | -0,5 | 0 | 0,5 | 1 | 2 |
| f'(x) | - | 0 | + | 0 | - | 0 | + |
Vi kan nu komplettera vår tidigare figur ovan med den nya informationen från vår teckenstudie. Vi vet nu hur kurvan lutar mellan punkterna där derivatan är lika med noll. Utöver det vet vi också hur kurvan lutar när vi går till vänster om den extrempunkt som ligger längst till vänster och till höger om den som ligger längst till höger.
Kurvan bör alltså likna den i följande figur:
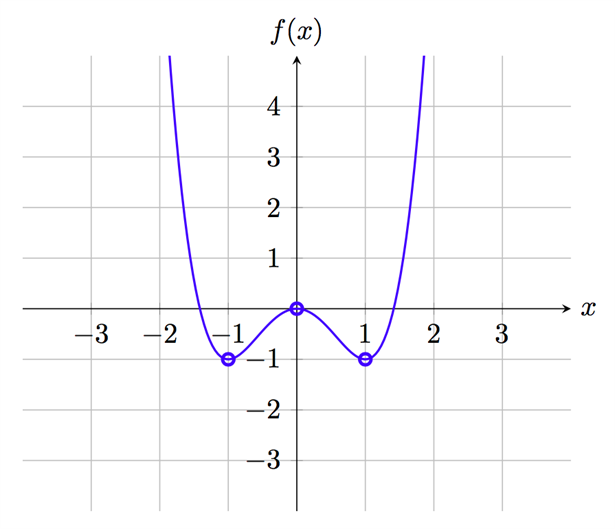
I det här läget får vi se upp så att vi inte råkar dra den förhastade slutsatsen att största funktionsvärdet är f(0), bara för att vi hade en maximipunkt där. I uppgiften söktes det största funktionsvärdet inom intervallet
$$-1< x\leq 2$$
Eftersom kurvan är växande till höger om extrempunkten (1,-1), så måste vi kontrollera hur stort det största funktionsvärdet är inom intervallet
$$1< x\leq 2$$
Utifrån vad vi vet om kurvans lutning i detta intervall, kommer det största funktionsvärdet naturligtvis att finnas i den punkt på kurvan där x=2. Vi beräknar därför f(2) och kollar om det blir större än f(0):
$$f(2)=2^{4}-2\cdot 2^{2}=16-8=8$$
Här har vi alltså hittat det största funktionsvärdet i intervallet: y=8 (i punkten där x=2).
Exempel 2:
En fyrhörning med räta vinklar, dvs en rektangel har omkretsen 10 m. Bestäm fyrhörningens sidor så att arean blir så stor som möjligt. Bestäm också arean, sidornas definitionsmängd och areans värdemängd.
Lösning: Vi ritar en figur, där vi döper längden av kortsidorna på rektangeln till x, de har alltså längden x meter. Eftersom omkretsen, summan av alla sidor, är 10 meter blir långsidornas längd tillsammans 10-2x och var för sig blir en långsida 5-x meter.

Nu kan vi skapa en funktion som beskriver arean av rektangeln, alltså basen multiplicerat med höjden, som vi betecknar \(A(x)\). Här är det viktigt att vi tar \(5-x \) i parantes så hela den längden blir multiplicerat med \(x\).
$$A(x)= x \cdot (5-x) = 5x-x^2$$
Här kan vi gå vidare på två sätt
- Lösa derivatans nollställen och därigenom beräkna arean.
- Areafunktionen \(A(x)\) är en negativ andragradsfunktion med symmetrilinjen \(x = -\frac{p}{2}\) som kurvans maximum.
Vi går igenom båda sätten att lösa problemet och börjar med 1. och hittar derivatans nollställen genom att lösa ekvationen \(A'(x)=0\), men vi börjar med att hitta själva derivatan.
$$A'(x) = 5 - 2x$$
$$5-2x = 0$$
$$x=2,5$$
Alltså är de sidorna vi döpte till x 2,5 meter och de resterande blir 5-2,5 = 2,5 meter de också. Den maximala arean blir
$$A(2,5) = 6,25 \text{ m}^2$$
Vi testar det andra tillvägagångssättet 2. och hittar symmetrilinjen \(x = -\frac{p}{2}\). Notera att vår funktion är \(A(x) = -x^2 +5x\) och för att hitta \(p\) måste det vara "tomt" (eller bara en ensam etta) framför \(x^2\), så vi delar hela funktionen med -1 och får att vårt \(p=-5\), som vi sätter in i formeln nedan
$$x = -\frac{p}{2} = - \frac{-5}{2} = 2,5$$
Alltså utgör x = 2,5 symmetrilinjen och kommer ge oss vår maximala area
$$A(2,5) = 5 \cdot 2,5 - 2,5^2 = 12,5 -6,25 = 6,25 \text{ m}^2$$
Vi fick samma svar med båda metoderna, så du kan välja själv vilken du tycker är smidigast.
Svar:
Maximala area \(A = 6,25 \text{ m}^2 \)
Sidorna blev alla 2,5 meter
Definitionsmängd \(0<x<5\) och värdemängd \(0< A(x) < 6,25 \)
Exempel 3:
Den markerade fyrhörningen med räta vinklar i figuren nedan är inskriven mellan kurvan \(f(x) = 6-x^2\) och x-axeln, med sina båda översta hörn på kurvan. Kurvan är symmetrisk kring y-axeln. Bestäm fyrhörningens största area \(A_{max}\) samt tillhörande höjd (h) och bredd (b).

Lösning: Översta högra punkten som ligger på kurvan har koordinaterna nedan eftersom de ligger på kurvan
$$(x,y) = (x, f(x)) = (x, 6-x^2)$$
Notera från bilden att y-värdet utgör höjden. Arean av fyrhörningen kan tecknas som funktion av x, symmetrin ger:
$$A(x) = 2xh = 2x(6-x^2)$$
För att ta reda på \(A_{max}\) deriverar vi först \(A(x)\) och bestämmer dess nollställen.
$$A(x) = 2x(6-x^2) = 12x -2x^3$$
$$A'(x) = 12 -6x^2$$
$$12-6x^2 = 0$$
$$-6x^2= -12$$
$$x^2 = 2$$
$$x= \pm \sqrt{2}$$
Maximala arean blir alltså när vi sätter in \(\sqrt{2}\) i \(A(x)\)
$$A(\sqrt{2})= 12\sqrt{2}-2{\left(\sqrt{2}\right)}^3 = 8 \sqrt{2}$$
höjden blev \(h = 6 - {\left(\sqrt{2}\right)}^2=4\)
Svar:
$$A_{max}=8 \sqrt{2} \text{ a.e. }$$
$$h=4 \text{ l.e.}$$
Förklaring till hur vi kan skissa grafer med hjälp av derivata.
- Definitionsmängd: de värden som en variabel som ingår i ett funktionsuttryck får anta, om vi har funktionen \(f(x)\) så är det alla x-värden som vi får stoppa in i funktionen
- Värdemängd: de värden som funktioner kan anta utifrån definitionsmängden, så om vi har en funktion så är det vad för y-värden vi får i grafen. Ett exempel kan vara \(f(x) = x^2\), vi får stoppa in vilka x-värden som helst, men funktionsvärdet som kommer ut blir alltid positiva värden och därför är värdemängden \(y \geq 0\)
- Derivata: en funktion som beskriver förändringshastigheten (lutningen) till en annan funktion
- Derivatans nollställen: vilka x-värden som löser ekvationen \(f’(x) =0\)
- Teckenstudie: en tabell där vi undersöker derivatans nollställen hur derivatan och själva funktionen beter sig kring dessa
- Maximipunkt: en punkt på grafen som utgör en vändpunkt, där grafen växer innan och avtar efter. På en parabel är detta det högsta värdet som grafen når, vid en maximipunkt är derivatan lika med noll
- Minimipunkt: en punkt på grafen som utgör en vändpunkt, där grafen avtar innan och växer efter. På en parabel är detta det minsta värdet som grafen når, vid en minimipunkt är derivatan lika med noll
- Terrasspunkt: en punkt på grafen som är som en platå, först växer grafen och sedan är den platt, (lutningen och derivatan är lika med noll) och sen växer den igen, eller först avtagande och platt och sen avtagande igen
- Extrempunkter: minimi- och maximipunkter är extrempunkter, det vill säga när derivatan är lika med 0
- Andraderivata: betecknas \(f’’(x)\) och uttalas ”f biss av x” och vi får det genom att derivera en funktion två gånger, dvs först derivera och sen hitta derivatan av funktionens derivata.
- Konkav graf: om andraderivatan har ett negativt värde för en punkt \(x=a\), dvs \(f’’(a) <0\) så är funktionen \(f(x)\) konkav kring punkten \(x=a\)
- Konvex graf: om andraderivatan har ett positivt värde för en punkt \(x=a\), dvs \(f’’(a) >0\) så är funktionen \(f(x)\) konvex kring punkten \(x=a\)
- Inflexionspunkt: när en funktion går från att vara konvex till konkav eller tvärtom, vi kan hitta inflexionspunkter då andra derivatan kommer vara lika med noll, \(f’’(x) = 0\)
