Största och minsta värde
I det förra avsnittet undersökte vi växande och avtagande funktioner och hur sådana förändringar hänger ihop med derivatan i olika punkter på en kurva.
Nu ska vi titta närmare på ett av de fall som vi hittade i det förra avsnittet - fallet då derivatan är lika med noll och tangenten i en sådan punkt alltså är horisontell (den är parallell med x-axeln). Vi ska även titta närmare på när en funktion antar sitt största eller minsta värde.
Derivatans nollställen
Varför är just sådana punkter där derivatan är lika med noll särskilt intressanta? Jo, om derivatan är noll och tangenten alltså är horisontell med x-axeln, då betyder det att vi på kurvan befinner oss högst uppe på en "topp" (vad vi i fortsättningen kommer att kalla en maximipunkt), längst ner i en "dal" (en minimipunkt) eller på en "terrass" (en terrasspunkt). En terrasspunkt är en punkt som på båda sidor om sig har en växande kurva eller på båda sidor en avtagande kurva.
Ett gemensamt begrepp som används för maximi- och minimipunkter är extrempunkter, eftersom vi i dessa punkter har funktionsvärden som är högre (maximipunkt) alternativt lägre (minimipunkt) än omgivande funktionsvärden för kurvan.
I figurerna nedan visar vi exempel på hur maximipunkter, minimipunkter och terrasspunkter kan se ut
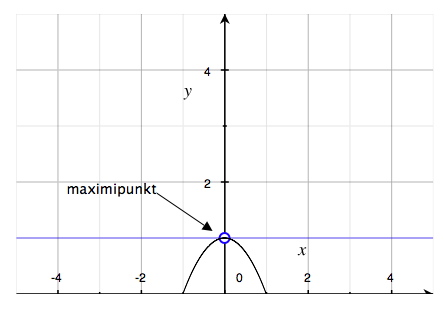
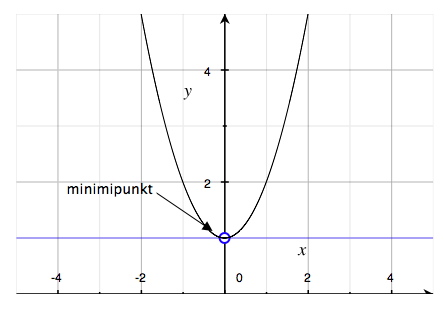
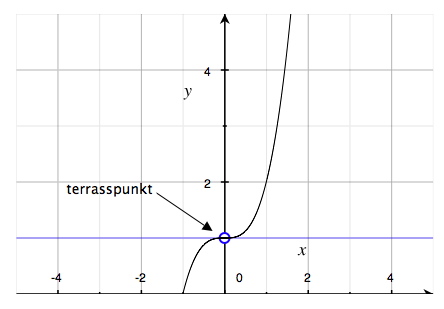
Några typiska funktioners grafer
Vi kan ha nytta av att känna igen och känna till huvuddragen i hur en polynomfunktion av högre grad ser ut. Det finns där två saker som är viktiga att notera och som är de dominerande faktorerna för grafens utseende. Det första är tecknet på koefficienten före termen med den största exponenten (positiv eller negativ), det andra är hur stor den största exponenten är. Vi visar nedan tre exempel på grafer med olika största exponent.
x2 - kurvor
Positiv koefficient framför x2

Negativ koefficient framför x2
x3 - kurvor
Positiv koefficient framför x3

Negativ koefficient framför x3

x4 - kurvor
Positiv koefficient framför x4

Negativ koefficient framför x4

Lokala extrempunkter och extremvärden
En funktion kan anta sitt största eller minsta värde i extrempunkter (maximipunkter eller minimipunkter) eller i intervallets ändpunkter. En funktion kan vara definierad för ett visst intervall och det är i början och slutet av intervallet som är intervallets ändpunkter.
Vi tittar närmare på funktionen nedan och dess graf. Vi vill undersöka funktionens extrempunkter, extremvärden och om den har ett största eller minsta värde.
$$f(x)=x^{3}+2x^{2}+2$$
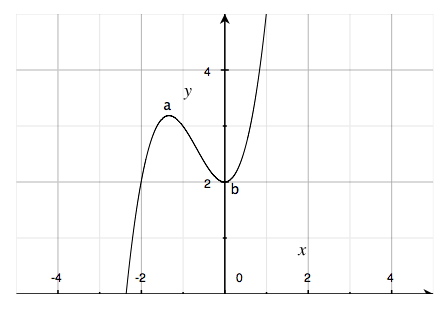
I denna graf har vi markerat ett maximivärde (a) och ett minimivärde (b). Vi vet att (a) och (b) är extrempunkter eftersom tangentens lutning i dessa punkter är horisontell och punkten (a) ligger på en "topp" och punkten (b) ligger i en "dal".
Vi kan hitta dessa punkters koordinater utifrån den information vi har om derivatan till funktionen. Eftersom det är extrempunkters koordinater vi söker, vet vi att tangenterna är utan lutning - derivatan i dessa punkter är lika med noll, vilket vi kan använda:
$$f'(x)=0$$
Vi behöver därför derivera funktionen, sedan sätta uttrycket lika med noll och sist lösa den ekvation vi får.
Först deriverar vi funktionen enligt de deriveringsregler som vi har kommit fram till tidigare:
$$f(x)=x^{3}+2x^{2}+2$$
$$f'(x)=3x^{2}+4x$$
Sedan sätter vi derivatan lika med noll:
$$0=3x^{2}+4x$$
Slutligen löser vi ekvationen (i det här fallet går ekvationen att lösa med nollproduktmetoden, vilket är det enklaste sättet när den är tillämpbar, men vi kan också lösa den med pq-formeln):
$$0=3x^{2}+4x$$
$$0=x(3x+4)$$
$$\begin{align} x_{1} & =0 \\ x_{2} & =-\frac{4}{3} \end{align}$$
Nu har vi hittat x-värdena för de båda extrempunkterna. Sätter vi in dessa x-värden i f(x) får vi också ut y-värdena i dessa punkter:
$$f(0)=0^{3}+2\cdot 0^{2}+2=2$$
Det ena extrempunkten (b), minimipunkten, ligger i (0,2).
$$f\left (-\frac{4}{3}\right )=\left ( -\frac{4}{3} \right )^{3}+2\cdot \left ( -\frac{4}{3} \right )^2 +2=$$
$$=-\frac{64}{27}+\frac{32}{9}+2=-\frac{64}{27}+\frac{96}{27}+\frac{54}{27}=$$
$$=\frac{86}{27}$$
Att beräkna funktionsvärdet för den andra extrempunkten (a), maximipunkten, var mer komplicerat, men till slut hittade vi den och kan konstatera att koordinaterna för punkten är (-4/3, 86/27), vilket är ungefär (-1,3; 3,2).
Vi kan nu svara på att det dessa värden för punkterna är varken det största eller minsta värde för funktionen. Om vi undersöker grafens utseende ser vi att funktionen fortsätter uppåt när vi går längst den positiva x-axeln och fortsätter neråt när vi går längst den negativa x-axeln. Detta fortsätter och funktionen har varken ett största eller minsta värde.
Exempel 1
Bestäm eventuella lokala extrempunkter, extremvärden och eventuella terrasspunkter till funktionen \(f(x)= 2x^3-3x^2\).
Vi börjar med att derivera \(f(x)\) och får
$$f'(x) = 2\cdot 3 x^2 -3\cdot 2x= 6x^2-6x$$
Extrempunkter finns där \(f'(x) =0\) så vi ställer upp och löser ekvationen
$$f'(x) = 6x^2 -6x = 0$$
$$6x(x-1) = 0$$
Vi får genom nollproduktsmetoden \(x_1 = 0 \) och \( x_2=1 \)
Vi skapar en teckenstudie för att bestämma karaktären på punkterna, genom att sätta in x-värden i derivatan, dessa x-värden är de för extrempunkterna och några punkter på sidan om och mellan dem för att se hur funktionen beter sig. Så först väljer vi x-värden, sätter in i derivatan och bryr oss bara om svaret blir positivt (då växer funktionen), negativt (då avtar funktionen) eller 0 (extrempunkt).
| \(x\) | \(-1\) | \(0\) | \(0,5\) | \(1\) | \(2\) |
| \(f'(x)\) | \(+\) | \(0\) | \(-\) | \(0\) | \(+\) |
| \(f(x)\) | växande | maximum | avtagande | minimum | växande |
Teckenstudien ger lokalt maximum för \(x=0\) och lokalt minimum för \(x=1\). Vi konstaterar att terrasspunkt saknas eftersom det då krävs att \(f'(x)\) ska vara antingen. positiv eller negativ på båda sidor om extrempunkten.
Svar:
Maximipunkten ges av \((0,f(0))= (0,0)\)
Minimipunkten ges av \((1,f(1))= (1,-1)\)
Terrasspunkt saknas.
Exempel 2:
Bestäm lokala extrempunkter, extremvärden och eventuell terrasspunkt till funktionen \(f(x) = 2x^3-18x\).
Lösning: Vi börjar med att söka extrempunkterna och deriverar funktionen och sätter derivatan lika med noll.
$$f'(x)= 6x^2-18$$
$$f'(x)= 6x^2-18=0$$
$$6x^2= 18$$
$$x^2 = 3$$
$$x_1 = \sqrt{3}$$
$$x_2 = -\sqrt{3}$$
Vi gör en teckenstudie för att bestämma karaktären på punkterna
| \(x\) | \(-2\) | \(-\sqrt{3}\) | \(0\) | \(\sqrt{3}\) | \(2\) |
| \(f'(x)\) | \(+\) | \(0\) | \(-\) | \(0\) | \(+\) |
| \(f(x)\) | växande | maximum | avtagande | minimum | växande |
Funktionens maximum fås i \(x= -\sqrt{3}\) och minimum i \(x = \sqrt{3}\), vi sätter in dessa x-värden i funktionen för att få ut punkternas y-värden.
$$f(-\sqrt{3})= 12\sqrt{3}$$
$$f(\sqrt{3})= -12\sqrt{3}$$
Svar: Extrempunkternas koordinater blir max \((-\sqrt{3},12\sqrt{3})\) och min \((\sqrt{3},-12\sqrt{3})\)
Exempel 3:
Betrakta funktionen \(f(x) = 3x^3+4x\). Har funktionen några extrempunkter eller terrasspunkter? Rita funktionen i ett koordinatsystem.
Lösning: För att ta reda på det börjar vi med att derivera funktionen
$$f'(x) = 9x^2 +4$$
och söker nollställena när \(f'(x) = 0\)
$$9x^2+4=0$$
$$x^2 = \frac{-4}{9}$$
Det betyder att derivatan saknar reella nollställen. I sin tur innebär det att funktionen \(f(x)\) saknar extrempunkter och terrasspunkt. En sådan funktion är antingen växande eller avtagande för alla x. Vilket värde på x vi än väljer så är \(f'(x)>0\). Det betyder att \(f(x)\) är strängt växande för alla x.
Vi kan också se i uppgiften att funktionen är en positiv tredjegradsfunktion eftersom \(x^3\)-termen är positiv.
Svar:
Funktionen saknar reella extremvärden och terrasspunkt.
Funktionsgrafen visas i figuren till höger.

Globala extrempunkter och extremvärden
Vi lärde oss i senaste avsnittet att avgöra funktioners lokala extrempunkter, extremvärden och terrasspunkter. Inom ett intervall a ≤ x ≤ b kan det finnas extrempunkter x som ger största och minsta värden antingen som lokala maximi- och minimipunkter eller som ändpunkter a och b i intervallet. I figurerna nedan visas två grafer som förtydligar olika extrempunkter.
I de fall a och b tillhör intervallet betecknas det med en ifylld punkt i ändpunkterna, om a och b inte tillhör intervallet är ändpunkterna inte ifyllda, vilket också betyder att funktionen inte är definierad i de punkterna. En sådan funktion saknar därför största och minsta värde i ändpunkterna. Då måste vi undersöka om det finns andra lokala maximi- eller minimipunkter hos funktionen.
Största och minsta värde betecknas även globalt maximum respektive globalt minimum (se figur). En funktion antar alltså sitt största eller minsta värde i derivatans nollställen eller i intervallets ändpunkter.

Huvuddragen av grafen till en funktion kan konstrueras med hjälp av derivata och teckenstudie. Genom teckenstudie av derivatan på båda sidor om derivatans nollställen, alltså där funktionen har extrempunkter, kan vi avgöra om funktionen är växande eller avtagande. Är derivatan positiv är funktionen växande, är derivatan negativ är funktionen avtagande. På så sätt kan vi få vägledning att skissa grafen till en funktion. Att skissa grafer beskrivs mer i detalj i ett senare avsnitt.
Ett exempel på teckentabell till en funktion som är definierad i intervallet -2 ≤ x ≤ 6 visas nedan. Lägg märke till att ändpunkterna ingår i intervallet och att vi har en terrasspunkt i \(x=0\), där\( f'(0)=0\) eftersom \(f'(x)\) har negativa värden på båda sidor om \(x=0\) . Största värde i intervallet är 10 och minsta är -14
Exempel 4: En funktion som begränsas av ett intervall
I det här exemplet tittar vi närmar på funktionen:
$$f(x)=x^3+3x^2$$
Som är begränsad i intervallet \(-4 \leq x\leq 2\).
Vi vill ta reda på det största och minsta värdet till funktionen som är definierat i intervallen ovan. Vi börjar med att ta reda på extremvärdena för funktionens extrempunkter. Det görs genom att först derivera och sätta derivatan till 0:
$$f'(x)=3x^2+6x$$
$$\begin{align} 3x^2+6x & =0 \\ x(3x+6) & =0 \end{align}$$
Här har vi två faktorer som ska vara lika med 0, det betyder att vi kan avläsa första faktorn och se att x1=0, för den andra gäller:
$$\begin{align} 3x+6 & =0 \\ 3x & = -6 \\ x_2 & =-2\end{align}$$
Vi har alltså hittat två x-värden till de extrempunkter som vi söker. Vi letar nu efter extremvärdena (y-värdena) i dessa två punkter. Det görs genom att stoppa in de funna x-värdena i funktionen:
För x1=0:
$$f(0)=0^3+3\cdot 0^2 = 0$$
För x2=-2:
$$f(-2)=(-2)^3+3\cdot(-2)^2=-8+12=4$$
Detta ger att vi har extremvärden i punkterna, vilka är y1=0 (som är kandidat för att vara det minsta värdet) och y2=4 (som är kandidat för att vara det största värdet).
För att vara säkra på om dessa extremvärden är de största eller minsta värdena för funktionen måste vi även testa intervallets ändpunkter, nämligen då x=-4 och x=2:
$$f(-4)=(-4)^3+3\cdot (-4)^2=-64+48=-16$$
$$f(2)=2^3+3\cdot 2^2=8+12=20$$
De största och minsta värdena till funktionen låg alltså inte i extrempunkterna, utan i intervallets ändpunkter. Det största värdet är 20 och det minsta värdet är -16.
Här går vi igenom extrempunkter och extremvärden.
Här går vi igenom hur vi hittar det största och minsta värdet för en funktion i ett intervall.
- Derivata: en funktion som beskriver förändringshastigheten (lutningen) till en annan funktion
- Derivatans nollställen: vilka x-värden som löser ekvationen \(f’(x) =0\)
- Teckenstudie: en tabell där vi undersöker derivatans nollställen hur derivatan och själva funktionen beter sig kring dessa
- Maximipunkt: en punkt på grafen som utgör en vändpunkt, där grafen växer innan och avtar efter. På en parabel är detta det högsta värdet som grafen når, vid en maximipunkt är derivatan lika med noll
- Minimipunkt: en punkt på grafen som utgör en vändpunkt, där grafen avtar innan och växer efter. På en parabel är detta det minsta värdet som grafen når, vid en minimipunkt är derivatan lika med noll
- Terrasspunkt: en punkt på grafen som är som en platå, först växer grafen och sedan är den platt, (lutningen och derivatan är lika med noll) och sen växer den igen, eller först avtagande och platt och sen avtagande igen
- Extrempunkter: minimi- och maximipunkter är extrempunkter, det vill säga när derivatan är lika med 0.
