Polynomfunktioner
Nu ska vi gå igenom grafers utseende för olika funktioner.
En förstagradsfunktion har alltid en graf som är en rät linje, medan en andragradsfunktions graf alltid är en parabel. Vi kan om vi vill beteckna polynomfunktioner med \(p(x)\) men kommer oftast välja \(f(x)\).
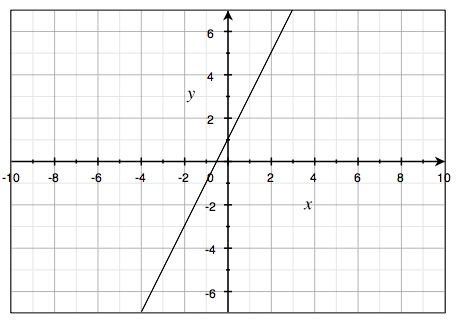
En av de polynomfunktioner som vi sett tidigare är en förstagradsfunktion
$$p(x)=2x+1$$
Denna funktions graf utgörs mycket riktigt av en rät linje:
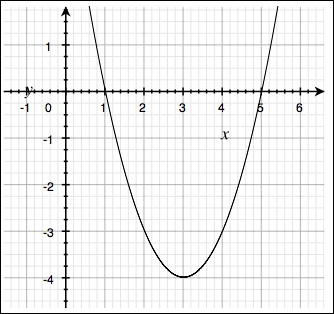
Ett annat exempel på polynomfunktion är denna andragradsfunktion:
$$p(x)=x^{2}-6x+5$$
Denna funktions graf ser ut så här:
Nu ska vi titta närmare på egenskaper hos polynomfunktioner också med högre gradtal än två.
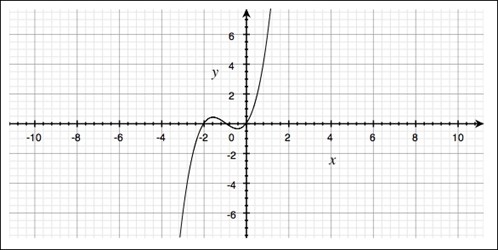
Ett exempel på en polynomfunktion av tredje graden är
$$ f(x)=x^{3}+3x^{2}+2x$$
Ett polynoms grad har stor betydelse för grafens utseende, vilket vi kan se om vi jämför graferna för funktionen av första graden och funktionen av andra graden. Här nedan ser du hur denna tredjegradsfunktions graf ser ut:
En förstagradsfunktion, vars graf utgörs av en rät linje, har alltid exakt ett nollställe, vilket är där linjen skär x-axeln.
Som vi kom fram till i ett tidigare avsnitt kan andragradsfunktioner ha antingen två, ett eller inget nollställe, vilket motsvaras av antalet gånger som kurvan skär x-axeln.
En tredjegradsfunktion kan ha som mest tre nollställen, vilket är fallet för exempelfunktionen ovan - ur grafen kan vi se att kurvan skär x-axeln vid x1=-2, x2=-1 och x3=0.
Generellt gäller det att en polynomfunktion p(x) av grad n har som högst n nollställen. En polynomekvation av grad n har på motsvarande sätt högst n rötter.
Beroende på hur ett polynomuttryck ser ut, kan man använda sig av antingen en grafisk metod för att hitta polynomfunktionens nollställen (vilket vi gjort i det här avsnittet) eller så kan man använda sig av en algebraisk metod där man letar efter polynomekvationens rötter. Ofta använder man sig av en kombination av lösningsmetoder.
Lösning av en tredjegradsfunktion grafiskt och algebraiskt.
- Rät linje, rät funktion: En funktion med ekvationen på formen \(y = kx+m\), vars graf kännetecknas av en rät (rak) linje
- Parabel: kurvan som bildas av en andragradsfunktion
- Polynom: ett algebraiskt uttryck med variabler och konstanttermer, där variablerna får endast ha exponenter som är positiva heltal. exempelvis är \(3x^2-4\) och \(-3x^7+0,8x^4-120\) polynom, medan \(x^{0,3}+4\) och \(5x^{-4}+x^2\) inte är det.
- Grad: högsta värdet på exponenten till variabeln i ett polynom, exempelvis har polynomet \(7x^4 -3x^2+x-3\) grad 4
- Nollställen: motsvarande till rötter fast för grafen, det vill säga var grafen skär x-axeln
