Enhetscirkeln

I det förra avsnittet repeterade vi rätvinkliga trianglar och sambanden mellan spetsiga vinklar i en rätvinklig triangel och triangelns sidor.

Vi utvidgar nu tangens-, sinus- och cosinus-funktionerna från det föregående avsnittet till att vara definierade för vinklar som är godtyckligt stora. Vi använder oss här av något som kallas enhetscirkeln, som är ett sätt att åskådliggöra de trigonometriska funktionernas värden för olika vinkelvärden mot x-axeln. Enhetscirkeln är centrerad i origo och har radien 1 längdenhet. Vinkeln mäts hur den går motsols från x-axeln och vi delar även in de olika områdena indelade av x- och y-axeln i fyra olika kvadranter. Vi illustrerar detta i denna bild nedan.

Men hur läser vi av trignometriska värden från cirkeln? Jo, x- och y-koordinaterna för varje punkt på cirkelns periferi (omkrets) får vi genom att läsa av värdena längs x- och y-axlarna. Vi kan tänka oss en rätvinklig triangel med en vinkel t, med den närliggande kateten längs med x-axeln och den motstående kateten vertikalt sammanbindande punkten på cirkelns periferi med x-axeln, så får vi följande figur:

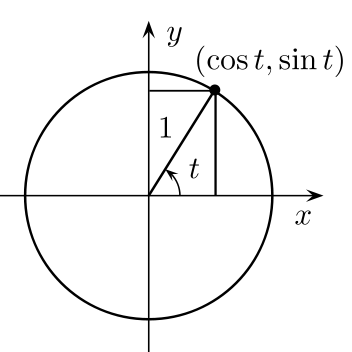
Om vi drar oss till minnes hur de trigonometriska funktionerna var definierade så har vi följande samband för sinus och cosinus för vinkeln t:

$$\sin t=\frac{y}{1}=y$$

$$\cos t=\frac{x}{1}=x$$

För att få en punkts x-koordinat använder vi därför cosinus för vinkeln; för att få punktens y-koordinat använder vi sinus för vinkeln. Punkten blir alltså (cos t, sin t). Nedan visar vi enhetscirkeln med några givna punkter och därmed trigonometriska värden. 

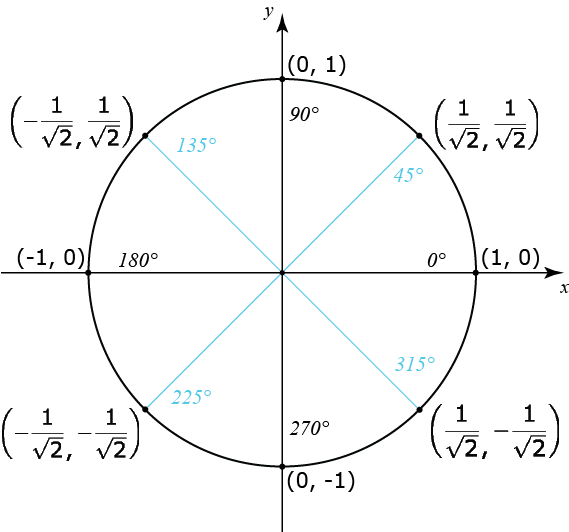
Vi kollar på några exempel hur vi kan använda enhetscirkeln för hitta vinklar och trigonometriska värden. 

Punkten B har koordinaterna \((0,92;0,40)\) vad är vinkeln \(v\)?

Vi kan använda antingen x- eller y –koordinaten för att hitta vinkeln v. Om vi tar x-koordinaten så vet vi att det motsvarar cosinusvärdet, dvs \(\cos(v) = 0,92\) och kan då applicera arccosinus på båda sidor och får då

$$v = \arccos(0,92)$$

$$v \approx 23,7^{\circ}$$

Vinkeln är därför 23,7°. Vi kan kontrollera genom att beräkna \(\arcsin(0,40)\) och även det ger oss \(v \approx 23,7^{\circ}\) .

Vi tar ett exempel till där vi kan se samband med hjälp av enhetscirkeln.

Utifrån enhetscirkeln, hitta koordinaterna till B.

Från den streckade linjen kan vi se att B har gemensamt y-värde med punkten till vänster, sen tack vare symmetrin i enhetscirkeln kommer x-värdet vara samma som vänstra punkten men byt tecken. Därför blir \(B: (0,6 ; 0,8)\).

Trigonometriska samband

Vi använder oss av enhetscirkeln för att visa två trigonometriska samband som vi kommer använda oss av i kommande avsnitt.

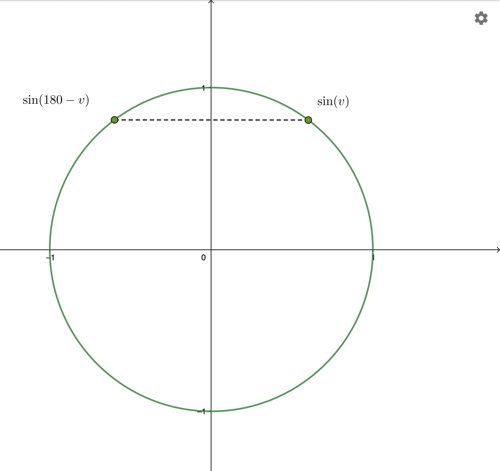
Punkterna delar samma y-värde och har därför samma sinusvärde.

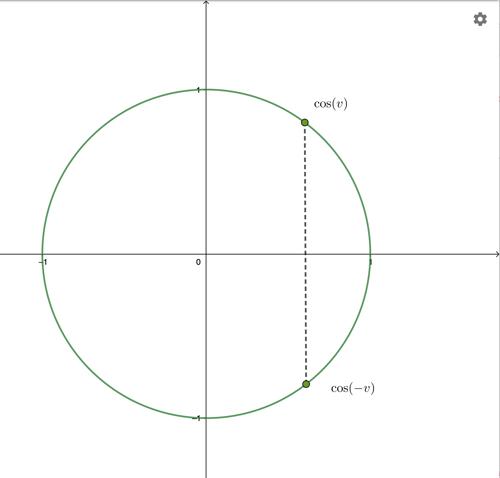
Punkterna delar samma x-värde och har därför samma cosinusvärde.

Sammanfattningsvis vet vi 

I enhetscirkeln får vi punkten koordinater (cos(v), sin(v)) där v är vinkeln som skapas motsols mot x-axeln.

$$\sin(v) = \sin(180-v)$$

$$\cos(v) = \cos(-v) $$

Nedan har vi en interaktiv enhetscirkel från GeoGebra, testa att dra runt vinkeln för att se hur olika punkter på cirkeln visar värdena för cosinus och sinus av vinkeln.

Videolektioner

Här går vi igenom enhetscirkeln och hur vi kan använda den tillsammans med sinus, cossinus och tangens.

En förklaring till enhetscirkeln och hur vi läser av värden med hjälp av den.