Sinussatsen

I det förra avsnittet stötte vi på areasatsen, som vi kan använda för att beräkna en triangels area om vi känner till längden på två av dess sidor och den mellanliggande vinkeln.

I det här avsnittet ska vi lära oss en annan triangelsats, i det här fallet en sats, sinussatsen, som beskriver förhållandet mellan triangels sidor och dess vinklar.

Vi använder oss av samma triangel som i det förra avsnittet:

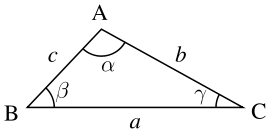
Sinussatsen lyder:

$$\frac{\sin \alpha}{a}=\frac{\sin \beta }{b}=\frac{\sin \gamma }{c}$$

Något som man inte bör missa är att a är den sida som ligger på motsatta sida från vinkeln α i figuren; på samma sätt ligger sidan b mittemot vinkeln β, och sidan c ligger mittemot vinkeln γ.

Vi kollar direkt på beviset för sinussatsen och vi kommer använda oss av areasatsen för alla tre vinklar, för den ger oss att arean av denna triangel oavsett vinkel vi utgår ifrån följande : (vi betecknar triangelns area med T eftersom vi använder stora A för hörnet av triangeln redan)

$$T = \frac {cb\cdot \sin(\alpha)}{2}=\frac{ca\cdot\sin(\beta)}{2}=\frac{ab\cdot\sin(\gamma)}{2}$$

Vi multiplicerar alla uttryck med 2 för att bli av med 2 i nämnaren och får då

$$2T =cb\cdot\sin(\alpha)=ca\cdot\sin(\beta)=ab\cdot\sin(\gamma)$$

Som sista steg delar vi hela uttrycket med abc och har du kvar

$$\frac{2T}{abc}=\frac{\sin \alpha}{a}=\frac{\sin \beta }{b}=\frac{\sin \gamma }{c}$$

Vilket är sinussatsen, som vi ville komma fram till. Första termen med arean behöver vi inte använda, det intressanta är att sinus av vinkeln delat på motstående sida förhåller sig på samma sätt med alla vinklar i triangeln.

Ett vanligt sätt att använda sinussatsen är om vi till exempel känner till de två sidorna a och b, och en av vinklarna α eller β, då kan vi skriva om sinussatsen, så att just den okända vinkeln kan beräknas direkt:

Känner vi till sidorna a och b, och vinkeln α, och vill veta vinkeln β, så kan man beräkna β så här:

$$\sin (\beta) = {\frac{b\cdot \sin(\alpha)}{a}}$$

$$\beta = \arcsin \left ( {\frac{b\cdot \sin(\alpha)}{a}} \right )$$

På liknande sätt kan man skriva om sambandet och lösa ut antingen en av triangelns sidor eller en av dess vinklar.

Låt oss ta ett konkret exempel på hur det kan bli

En triangel har en vinkel som är 50° med motstående sida som är 5 cm. En annan sida i samma triangel är 4 cm. Hur stor är vinkeln motstående till sidan som är 4 cm?

Om vi betecknar den kända vinkeln α = 50° och den okända vinkeln β, och sidorna a = 5 cm och b = 4 cm, så gäller enligt sinussatsen följande samband:

$$\frac{\sin(50^\circ)}{5}=\frac{\sin (\beta)}{4}$$

Skriver vi om denna trigonometriska ekvation, så får vi detta:

$$\beta = \arcsin\left ( {\frac{4\cdot \sin(50^\circ)}{5}} \right )$$

$$\beta \approx 37,8^\circ $$

Men denna trigonometriska ekvation har som vi sett förr en till lösning, därför är också denna vinkel en lösning.

$$\beta \approx 180^{\circ}- 37,8^\circ = 142,2^{\circ} $$

I nästa exempel ska vi leta efter en okänd sida. Vi har en triangel i bilden nedan med vinklarna 43° och 49° och sidan 7,7 cm, hitta sidan b.

Enligt sinussatsen kan vi ställa upp följande ekvation,

$$\frac{\sin(43^{\circ})}{7,7} = \frac{\sin(49^{\circ})}{b}$$
vi beräknar värdet för båda sidor

$$0,08857…= \frac{0,75471…}{b}$$

nu multiplicerar vi båda sidor med b och sedan dividerar med 0,08857… och får

$$b\approx 8,5$$

Alltså är sidan b ca 8,5 cm.

Vi tar ett till exempel, beräkna sidorna i triangeln nedan.

Vi börjar med att beteckna motstående sida från hörnet A till a och motstående sida till B till b och nu kan vi ställa upp ekvationen

$$\frac{\sin(37^{\circ})}{5,6} = \frac{\sin(67^{\circ})}{b}$$
vi beräknar värdet för båda sidor

$$0,1075…= \frac{0,9205…}{b}$$

nu multiplicerar vi båda sidor med b och sedan dividerar med 0,1075… och får

$$b\approx 8,6$$

Vi gör nu samma sak för att få ut a

$$\frac{\sin(37^{\circ})}{5,6} = \frac{\sin(76^{\circ})}{a}$$

$$0,1075…= \frac{0,9703…}{a}$$

$$a\approx 9,0$$

Vi får därför ut att resterande sidor i triangeln är 8,6 cm och 9,0 cm.