Dragning utan återläggning
En urna innehåller 4 svarta och 6 vita kulor. Två kulor dras slumpmässigt utan återläggning. Beräkna sannolikheten att få
a) 2 svarta kulor
b) 2 vita kulor
c) 1 svart och 1 vit kula
Gör ett träddiagram. Sannolikheterna i varje gren beror av vad för kula man drog innan. Har man t.ex. dragit en svart, så är det 1 svart mindre och totalt 1 färre i urnan.
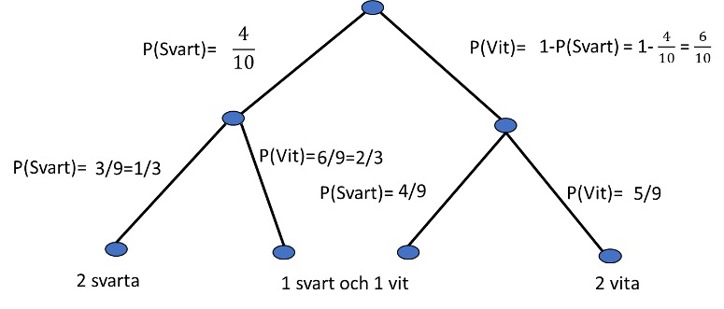
a) P(S, S) = P(1 svart i första dragning) \(\cdot\) P(1 svart i andra dragning)
\[P(S, S) = \frac{4}{10}\cdot \frac{3}{9} = \frac{2}{5}\cdot \frac{1}{3} = \frac{2}{15}\]
b) P(V, V) = P(1 vit i första dragning) \(\cdot\) P(1 vit i andra dragning)
\[P(V, V) = \frac{6}{10} \cdot \frac{5}{9} = \frac{3}{5} \cdot \frac{5}{9}) = \frac{1}{3}\]
c) 1 svart och 1 vit: P(S, V) = P(V, S) = P(S, V) + P(V, S)
\[P(1\; \text{svart och}\;1\; \text{vit}) = \frac{4}{10}\cdot \frac{6}{9} + \frac{6}{10}\cdot \frac{4}{9} = \frac{3}{5}\cdot \frac{5}{9} = \frac{8}{15}\]
Svar:
a) P(2 svarta) \(= \frac{2}{15}\)
b) P(2 vita) \(= \frac{1}{3}\)
c) P(1 vit och 1 svart) \(= \frac{8}{15}\)
