Ändringskvot

Ofta är vi intresserade av att få veta hur ett värde har förändrats under en viss tid. Det kan till exempel vara hur temperaturen har förändrats i en termos under 5 timmar, eller hur en befolkningsmängd har ökat eller minskat under 10 års tid. Hur kan vi ta reda på det?

Exempel på ändringskvot
I följande figur ser vi en stigande kurva som illustrerar hur ett föremål rört sig upp i luften.

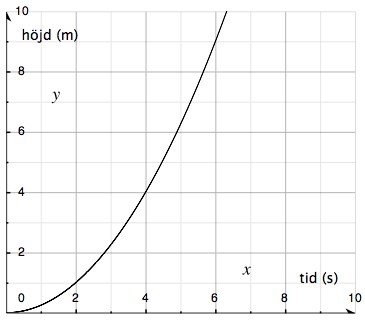
Vi kan läsa av direkt i figuren till exempel på vilken höjd föremålet befann sig vid en viss tidpunkt, eller omvänt hur många sekunder det tog för föremålet att nå en viss höjd.

Men hur stor var höjdökningen i genomsnitt till exempel i tidsintervallet 2 till 6 sekunder? Vi kan läsa av att höjden har gått från 1 meter (vid tiden 2 sekunder) till 9 meter (vid tiden 6 sekunder). Detta är skillnaden i y-led. Skillnaden i x-led är 4 sekunder.

I figuren nedan kan vi se de två punkterna (2, 1) och (6, 9) markerade. Vi kan också se skillnaden i x-led och i y-led mellan dessa punkter på kurvan. I blått har vi även dragit en rät linje mellan dessa båda punkter på kurvan. En sådan rät linje som skär en kurva i minst två punkter kallas en sekant.

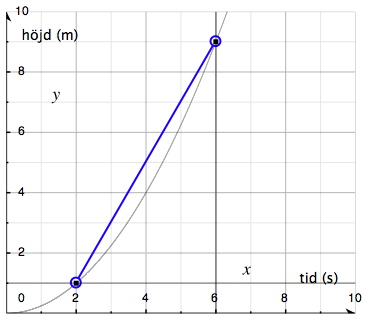
Den genomsnittliga höjdökningen under tidsperioden 2 till 6 sekunder får vi genom att dividera höjdskillnaden med tidsskillnaden:

$$\frac{y_2-y_1}{x_2-x_1}=\frac{9-1}{6-2}=\frac{8}{4}=2 \;meter \;per \;sekund$$

Notera att detta är samma formel som vi använder då vi räknar ut riktningskoefficienten (k) för en rät linje mellan punkterna. Genom att beräkna lutningen på sekanten kan vi alltså ta reda på den genomsnittliga förändringshastigheten i ett intervall (mellan de två punkterna).

Den genomsnittliga förändringshastigheten kallas också ändringskvot och är lika med kurvans genomsnittliga lutning i ett visst intervall.