Derivatans h-definition

Vi har i tidigare avsnitt ställt upp ändringskvoter och beräknat gränsvärden. Nu ska vi ställa upp ett generellt uttryck som gäller för alla gränsvärden. Vi föreställer oss en generell funktion y = f(x), och sätter ut en godtycklig punkt med koordinaten (x, f(x)):

Vi sätter sedan, på samma sätt som vi gjort tidigare, ut en ytterligare punkt, som ligger på avståndet h från den första punkten (x, f(x)). Denna andra punkt får koordinaterna ( (x+h), f(x+h) ):

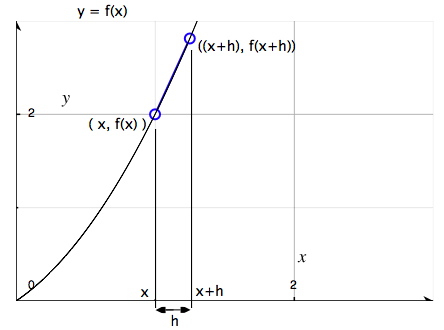
k-värdet för linjen som sammanbinder dessa båda punkter blir:

$$k=\frac{f(x+h)-f(x)}{(x+h)-x}=\frac{f(x+h)-f(x)}{h}$$

Om vi nu låter den högra punkten ( (x+h), f(x+h) ) ligga närmare och närmare den vänstra (x, f(x)), så innebär det att vi låter h gå mot noll:

$$h\rightarrow 0$$

(Detta är samma tankegång som i avsnittet om tangentens lutning, där vi definierade formeln för ändringskvoten, men då utgick vi från en specifik punkt (2, f(2)) och lät den andra punkten (x, f(x)) närma sig den första punkten genom att x gick mot 2.)

Gränsvärdet för (x, f(x)) blir:

$$k=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{(x+h)-x}=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$$

Detta uttryck kallas för derivatans h-definition.

Vill vi använda denna formel för att beräkna derivatan av funktionen f i den punkt där x=a, alltså f´(a), så blir alltså formeln:$$f{}'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$$

$$f'(a)=\lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h}$$

Videolektioner

Här går vi igenom derivatans h-definition.

Derivera med derivatans h-definition.