Areasatsen

I tidigare avsnitt har vi använt trigonometri för räta trianglar, nu går vi vidare till användning av godtyckliga trianglar, som kan ha vilka vinklar som helst. Vi behöver också ha med oss från Matte 1-kursen när vi lärde vi oss sambandet mellan en triangels area (A) och dess bas (b) och höjd (h):

$$A=\frac{b\cdot h}{2}$$

Det här sambandet innebär att om vi vill veta en triangels area så kan vi beräkna den om vi känner till dess bas och höjd. Men finns det något bra sätt att beräkna arean om vi inte känner till denna information? Ja, det kan vi göra med hjälp av areasatsen, som lyder:

$$Area=\frac{b\cdot c\cdot \sin (\alpha)}{2}$$

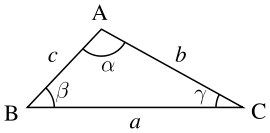
I areasatsen är b och c två av triangelns sidor och \(\alpha\) är den vinkel som ligger mellan dessa båda sidor, enligt triangeln nedan:

Om vi får en given area och två sidor och med hjälp av areasatsen istället vill hitta vinkeln mellan sidorna så kommer vi få en ekvation som tillslut kommer vara av typen \(\sin v = k\) där v kommer vara vinkeln vi letar efter och k någon konstant, och vi vet sen tidigare avsnittet om trigonometriska ekvationer att sinus kommer ha två lösningar mellan 0≤ v≤ 180°, vilket är möjliga vinklar i en triangel. Detta betyder att triangeln kan se ut på två olika sätt, med trubbig eller spetsig vinkel och vi får kontrollera om båda vinklarna är möjliga fall.

Bevis

Innan vi går vidare till att se på exempel hur vi använder areasatsen så kollar vi på ett bevis på hur vi kommer fram till areasatsen. Vi börjar med att rita upp en godtycklig (dvs med obestämda mått och vinklar) som vi markerat höjden på.

Vi vet sen innan att arean av denna triangel skulle bli basen (a) multiplicerat med höjden (h) och sen dividerat med 2, alltså

 $$ Area = \frac{ah}{2}$$

Nu vill vi uttrycka detta utan att använda höjden (h) och istället använda sinus.  Om vi tänker oss att triangeln blir uppdelad i två rätvinkliga trianglar av höjden, vi kollar specifikt på triangeln med hörnen ACD och vinkeln D är 90°. Vi har tidigare sett att förhållandet för sinus i rätvinkliga trianglar är att \(\sin v = \frac{ motstående}{hypotenusa}\) och i denna triangel blir det alltså \( \sin(C) = h/b\). Nu vill vi lösa ut h i detta uttryck eftersom det är den som ska bytas ut, så vi multiplicerar båda sidor med b och får då \(h = b \cdot sin(C)\).

Nu byter vi ut h i formeln för arean och får istället

$$Area = \frac{ ab \cdot \sin (C)}{2}$$

Vilket var det vi ville komma fram till, areasaten.

Låt oss nu kolla på några exempel på hur vi kan tillämpa areasatsen

Räkna ut arean för en triangel där ena sidan är 3 cm, en annan sida är 4 cm och den mellanliggande vinkeln är 50°.

Kallar vi sidorna a (3 cm) och b (4 cm), och den mellanliggande vinkeln γ (50°), kan vi använda areasatsen så här:

$$Area=\frac{3\cdot 4\cdot \sin (50^\circ)}{2}\approx 4,6 \: cm^2$$

Nu tittar vi på ett exempel där vi söker vinkeln. En triangel har sidorna 6 cm och 5 cm och arean 12 cm², vad är den mellanliggande vinkeln?

Vi sätter in våra värden i formeln för arean och får nu en trigonometrisk ekvation att lösa

$$12 = \frac{6\cdot 5\cdot \sin(A)}{2} $$
Vi multiplicerar med 2 och delar med 30 och får då

$$\sin(A) = 0,8$$

som vi såg i tidigare avsnitt om trigonometriska ekvationer behöver vi applicera arcsin på båda sidor och får

$$\arcsin(\sin(A)) = \arcsin(0,8)$$

$$A = 53,13^{\circ}$$

Eftersom vi inte fått någon information om hur triangeln ser ut och kan avgöra om vinkeln är spetsig eller trubbig. Därför får vi en till möjlig lösning

$$A_2= 180^{\circ}-53,13^{\circ} = 126,87^{\circ}$$

Svaret blir alltså att mellanliggande vinkeln är 53,13° eller 126,87°

Vi tittar på ett sista exempel där vi kan använda oss av areasatsen på ett nytt sätt. Beräkna arean på fyrhörningen

Vi delar upp fyrhörningen i två trianglar så här

Nu kan vi beräkna arean för båda trianglarna och sedan addera ihop dem, vi börjar med den undre triangeln och kallar den för Area₁

$$Area_1 = \frac{ 3\cdot 5,1\cdot \sin(103^{\circ})}{ 2} \approx 7,454 cm^2$$

Den övre triangeln, som får kallas Area₂, beräknar vi på samma sätt

$$Area_2 = \frac{ 4,7\cdot 2,7\cdot \sin(118,8^{\circ})}{2} \approx 5,560 cm^2$$

Fyrhörningens area blir då

$$ Area = 7,454+5,560 \approx 13,0 cm^2$$