Deriverbarhet

I det här avsnittet ska vi gå igenom vad som gör att en funktion är deriverbar och vilka situationer som gör att funktionen inte är deriverbar i en viss punkt.

Att en funktion är deriverbar i en punkt kan vi med ord förklara att det endast går att rita upp en tangent i den punkten. Det krävs att funktionen är definierad och kontinuerlig i punkten. Däremot finns det funktioner som är definierade och kontinuerliga i en punkt, men som ändå inte är deriverbara i punkten.

Definierad i en punkt

Att en funktion är definierad i en punkt betyder att punktens x-värde ingår i funktionens definitionsmängd. För att göra det lite tydligare kollar vi på två funktioner och deras deriverbarhet.

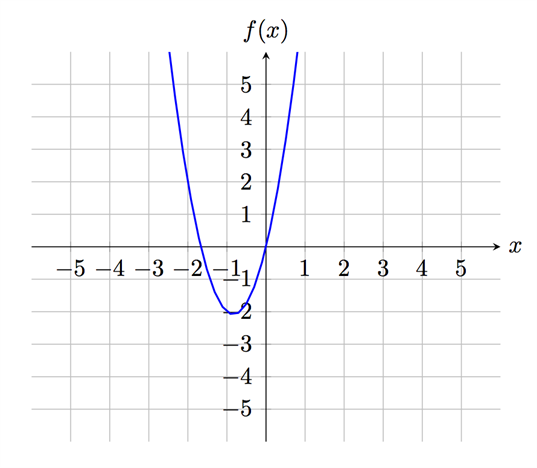
Vi har funktionen \(f(x)=3x^2+5x\). Denna funktion är definierad för alla x-värden, vilket betyder att den är deriverbar för alla x. Anledningen till att vi vet detta beror på att vi kan stoppa in alla x-värden i funktionen och få fram ett y-värde, alltså alla x-värden ingår i funktionens definitionsmängd.

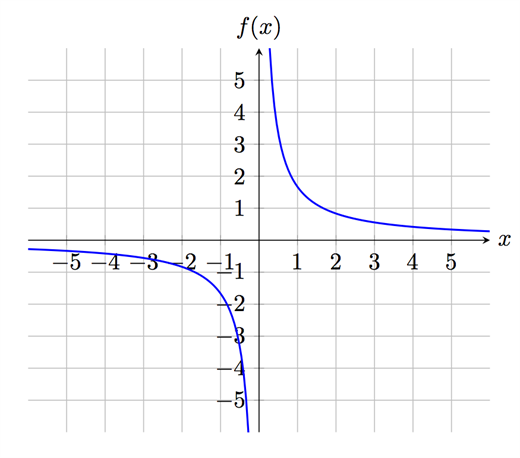
Har vi funktionen \(f(x)=\frac{5}{3x}\), kan vi se att den inte är definierad i punkten x = 0. Detta ser vi direkt eftersom funktionen är en kvot där nämnaren består av en multiplikation med ett x-värde. Om vi skulle ta x = 0 får vi \(\frac{5}{3\cdot 0}\), vilket är odefinierat. Funktionen är därför inte deriverbar när x = 0.

Kontinuerlig funktion

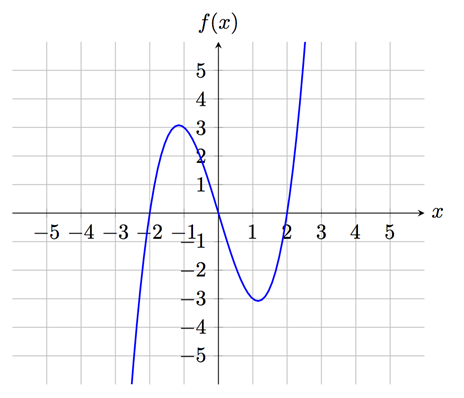
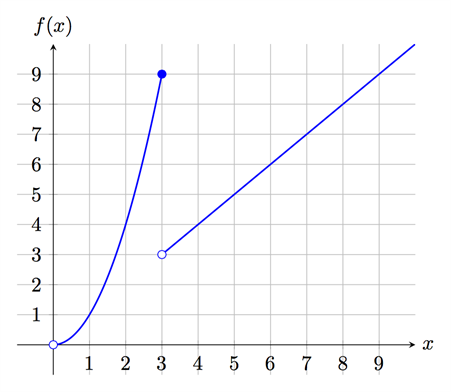
Att en funktion är kontinuerlig betyder att funktionens graf är sammanhängande. Ett annat sätt att tänka är att om vi kan rita upp funktionens graf utan att lyfta på pennan, då är funktionen kontinuerlig. Om funktionens graf inte är sammanhängande, då kallas den diskontinuerlig. Vi ritar upp två funktioner, där den första funktionen är kontinuerlig och den andra funktionen är diskontinuerlig.Allmänt så är en funktion inte deriverbar om den inte är kontinuerlig. Men det finns fall då funktionen är kontinuerlig, men ändå inte deriverbar, vilket vi ska titta på exempel på längre ner.

Att funktionen är kontinuerlig på sin definitionsmängd får betydelse i följande exempel:

Till exempel grafen av funktionen \(f(x)=\frac{5}{3x}\) hänger inte ihop, det betyder inte att funktionen är diskontinuerlig, utan funktionen är odefinierat i \(x=0\) (dvs. \(x=0\) inte tillhör definitionsmängden), alltså nämnaren får aldrig vara noll.

I så fall kan man säga att funktionen \(f(x)=\frac{5}{3x}\) är kontinuerlig för sin definitionsmängd.

Definierad och kontinuerlig, men inte deriverbar i en punkt

Som vi nämnde i inledningen till detta avsnitt finns det funktioner som är definierade och kontinuerliga i en punkt, men som ändå inte är deriverbara i punkten. Detta sker när vi har en funktion som exempelvis innehåller absolutbelopp. Vi kollar på grafen till funktionen \(f(x)=|x-2|\):

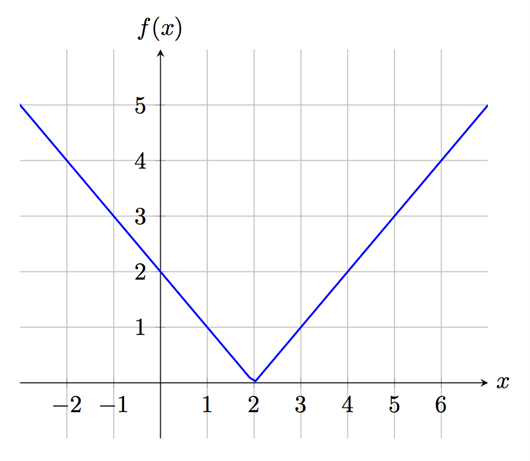
Som vi ser på bilden är funktionen spetsig vid punkten (2,0). I denna punkt är funktionen definierad och kontinuerlig, men inte deriverbar. Att den inte är deriverbar beror på att vi kan rita upp två tangenter i den punkten beroende på vilket håll vi närmar oss x-värdet 2. Närmar vi oss punkten (2,0) från vänstra sidan har vi en tangent med lutningen -1, men närmar vi oss punkten från högra sidan har vi en tangent med lutningen 1.

Vi kan komma fram till samma slutsats om vi ställer upp gränsvärdet för derivatan i punkten och undersöker om den existerar (vilket den inte kommer göra eftersom den inte är deriverbar).

Vi kan påminna oss från avsnittet om Gränsvärden att gränsvärden så som \(\lim_{x \to a} f(x) \) existerar om 

$$\lim_{x \to a} f(x) = \lim_{x \to a^{+}} f(x) = \lim_{x \to a^{-}} f(x)  $$

Där \(a^{+}\) betyder att vi närmar oss från höger och \(a^{-}\) från vänster. Vi använder detta och undersöker gränsvärdet för derivatan i en punkt:

$$f’(2) = \lim_{h \to 0} \frac{f(2+h)-f(2)}{h}$$

Vi undersöker detta genom att h närmar sig 0, från både vänster och höger. Vi börjar med -0,1 och 0,1 och sen mindre och mindre värden

Eftersom gränsvärdet både närmar sig -1 och 1 när h närmar sig noll så existerar det inte och inte heller en derivata i den punkten, när x = 2.

I nästa exempel tittar vi på en sammansatt funktion, där vi lappat ihop två funktioner för olika intervall.

Exempel:

Undersök om f(x) är kontinuerlig och deriverbar för x = 1

$$f(x) = \begin{cases} \sqrt{x+3} \text{ när }x>1\\ 2x \:\:\:\:\:\:\:\: \text{ när } x \leq 1\end{cases}$$

Lösning: Vi ritar upp grafen i GeoGebra med hjälp av funktion Om(Villkor, Då, Annars)

Då skriver vi x > 1 som ”Villkor” och då vill vi ha\( \sqrt{(x+3)}\) så det skriver vi under ”Då”. Sen eftersom  x≤1 blir ”Annars” och då skriver vi 2x, som i bilden nedan.

Då får vi detta, som var funktionen vi fick

Och grafen ser ut så här

Nu kan vi se att funktionen är kontinuerlig i punkten x = 1. Vi kan även undersöka i GeoGebra genom att skriva \(f(1)\) och får ut \(f(1) = 2\) och då är punkten kontinuerlig

För att undersöka om \(f(x)\) är deriverbar när \(x=1\), det vill säga att gränsvärdet för \(f’(1)\) existerar kan vi använda oss av GeoGebra igen, men denna gång är det viktigt att notera att vi har ett CAS-fönster öppet och inte bara grafräknare.

Vi använder oss av funktionen Gränsvärde( Uttryck, Variabel, Värde) och sätter in gränsvärdet, h som variabel och 0 som värde och får då ut ”?”, vilket betyder att gränsvärdet inte existerar och därför är funktionen inte deriverbar i x = 1.

Utifrån grafen kan vi också se att det blir en kant när de olika intervallen möts i \( x=1\), som inte kommer kunna ha en gemensam tangent.  

Sammanfattning

Icke kontinuerliga funktioner är inte deriverbara

För kontinuerliga funktioner som inte är deriverbara i punkten x=a existerar inte gränsvärdet
$$f’(a) = \lim_{h \to 0} \frac{f(a+h)-f(a)}{h}$$