Parabelns ekvation

I avsnittet om andragradsekvationer lärde vi oss att grafen till en andragrafsfunktion är en parabel. I det här avsnittet ska vi titta närmare på parabler och bestämma en parabels ekvation.

En andragradsfunktion kan alltid skrivas på formen

$$f(x)=ax^{2}+bx+c$$

där a, b och c är reella tal, och a ≠ 0.

En funktion som kan skrivas på denna form kommer att ha några intressanta egenskaper, såsom att värdet på konstanten a kommer att bestämma om grafen (parabeln) kommer att ha en minimipunkt eller en maximipunkt. Värdet på konstanten c anger var parabeln kommer att skära y-axeln. Allmänt gäller också att parabler alltid kommer att vara symmetriska runt en symmetrilinje; denna symmetrilinje ligger mittemellan funktionens eventuella nollställen (x₁ och x₂) och är markerad med en streckad röd linje i figuren nedan.

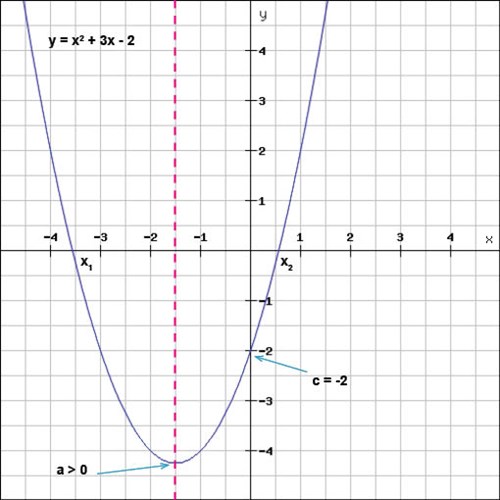
Utifrån att vi vet att varje andragradsfunktions graf är en parabel ska vi nu gå vidare och bestämma parabelns ekvation.

Fokuspunkt/brännpunkt och styrlinje

En parabel definieras av att det för varje punkt (P) som utgör del av parabeln gäller att avståndet från denna punkt till en viss fokuspunkt/brännpunkt (Q) är lika stort som till en viss styrlinje (S).

I koordinatsystemet nedan visar vi hur detta kan se ut i fallet då parabelns minimipunkt ligger i origo:

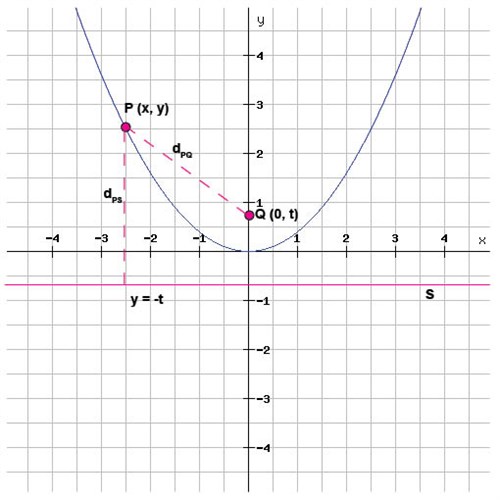
Av parabelns definition följer också att parabelns extrempunkt ligger mittemellan fokuspunkten och styrlinjen.

Var varje punkt som utgör parabeln ligger beror helt och hållet på var fokuspunkten respektive styrlinjen ligger. Känner man till fokuspunkten och styrlinjen kan man bestämma formen på parabeln.

Parabelns ekvation

Nu ska vi bestämma parabelns ekvation för fallet som visas i figuren ovan, då fokuspunkten Q har koordinaterna (0, t) och styrlinjen har ekvationen y = -t, där t är ett reellt tal.

Med dessa beteckningar kan vi med hjälp av avståndsformeln och parabelns definition komma fram till parabelns ekvation.

Vi vet ju nämligen att avståndet från en punkt P (x, y) ska vara lika stort till fokuspunkten som till styrlinjen. Detta gör att vi kan skriva två uttryck för dessa respektive avstånd och att dessa två uttryck ska vara lika stora.

Avståndsformeln lyder:

$$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$

Med denna formel kan vi beräkna avståndet mellan punkten P (x, y) och fokuspunkten Q (0, t):

$$d_{PQ}=\sqrt{(x-0)^2+(y-t)^2}=$$

$$=\sqrt{x^2+(y-t)^2} $$

På samma sätt kan vi beräkna avståndet mellan punkten P och styrlinjen S (vars kortaste avstånd till P är i den punkt på styrlinjen där x-värdet är detsamma som i punkten P):

$$d_{PS}=\sqrt{(x-x)^2+(y-(-t))^2}=$$

$$=\sqrt{(y-(-t))^2}=$$

$$=\sqrt{(y+t)^2}=$$

$$=y+t $$

Som vi kom fram till tidigare, vet vi att enligt parabelns definition så ska avstånden dPQ och dPS vara lika långa, vilket gör att vi kan ställa upp följande ekvation och ur ekvationen sedan försöka att lösa ut y:

$$d_{PQ}=d_{PS}$$

$$\sqrt{x^2+(y-t)^2}=y+t$$

Eftersom vi nu har ett rotuttryck i vänstra ledet kvadrerar vi båda leden:

$$\left (\sqrt{x^2+(y-t)^2} \right )^2=(y+t)^2$$

$$x^2+(y-t)^2=(y+t)^2$$

I det här läget kan vi utveckla det vänstra ledet genom att använda andra kvadreringsregeln och det högra ledet genom att använda första kvadreringsregeln. Därefter förenklar vi ekvationen genom att subtrahera termer som finns i både vänster och höger led enligt nedan:

$$ x^2+{\color{Blue} {y^2}}-2ty+{\color{Red}{t^2}}={\color{Blue}{ y^2}}+2ty+{\color{Red} {t^2}}$$

$$x^2-2ty=2ty $$

$$x^2=4ty$$

$$y=\frac{x^2}{4t}$$

Den ekvation som vi kom fram till här ovan är den allmänna formeln för ekvationen till en parabel som har sin extrempunkt i origo och fokuspunkten (0, t) och styrlinjen y = -t:

$$y=\frac{x^2}{4t}$$

Bestämning av fokuspunkt och styrlinje

Om vi har en känd andragradsfunktion, till exempel

$$y(x)=x^2$$

så kan vi med hjälp av parabelns ekvation beräkna var fokuspunkten måste ligga (vilket värdet på t måste vara, alltså fokuspunktens y-koordinat).

Anger vi helt enkelt att y-värdet ska vara detsamma och löser ut t, så får vi

$$\frac{x^2}{4t}=x^2$$

$$\frac{x^2}{4t\cdot x^2}=\frac{x^2}{x^2}$$

$$\frac{1}{4t}=1$$

$$1=4t$$

$$t=\frac{1}{4}=0,25$$

Fokuspunkten ligger alltså i (0; 0,25) för just denna parabel. Eftersom extrempunkten ska ligga mittemellan fokuspunkten och styrlinjen, får vi att styrlinjen ska ha ekvationen y = -0,25.

Ett konkret användningsområde för parabler som nog de flesta har träffat på är så kallade parabolantenner. Dessa antenner är designade utifrån kunskap om sambandet mellan parabelns utseende och fokuspunkten - inkommande strålar fokuseras genom antennens utformning till just fokuspunkten/brännpunkten, varigenom den mottagna signalen förstärks.