Uppgift 15
I en rätvinklig triangel \(ABC\) finns en grå kvadrat \(AEFD\) inritad. Sträckan \(BE\) är 4 cm och sträckan \(CD\) är 2cm. Se figur.
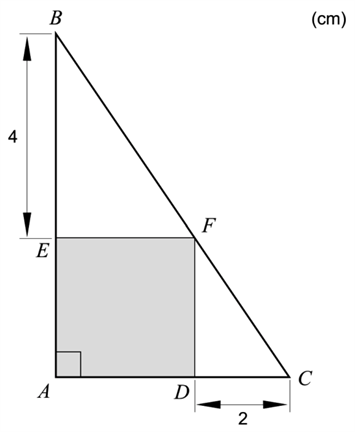
Visa att den grå kvadratens yta är 8 cm2.
Lösningsförslag
För att lösa uppgiften har vi ritat följande figur.
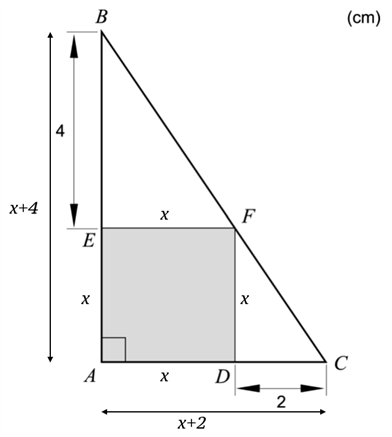
I figuren har vi satt att kvadratens sidor är \(x\). Arean som vi letar efter är \(A_{kvadrat}=x^2\) och det vi ska visa är att \(A_{kvadrat}=x^2=8\).
Från figuren ser vi att trianglarna \(BEF\) och \(FDC\) är likformiga. Det ger oss att förhållandet mellan motsvarande sidor i trianglarna är lika:
$$\begin{align} \frac{4}{x} & =\frac{x}{2} \\ 4\cdot 2 &= x\cdot x \\ 8 &= x^2 \end{align}$$
Vi har räknat ut att \(x^2=8\) och i början av lösningen sa vi att \(A_{kvadrat}=x^2\). Detta betyder att \(A_{kvadrat}=8\), alltså att kvadratens yta är 8 cm2, vilket skulle visas.
Uppgiften är hämtad ur "Kursprov Matematik 2c, vårterminen 2015" - Ladda ner provet här.
