Uppgift 21

Magnituden M är ett mått på hur starkt en stjärna lyser och kan beräknas med hjälp av formeln

$$M-5=a-5 \lg \left( \frac{r}{3\cdot 10^{16}} \right)$$

där \(r\) är avståndet i meter från jorden till stjärnan och \(a\) är en konstant för en specifik stjärna, se tabell nedan.

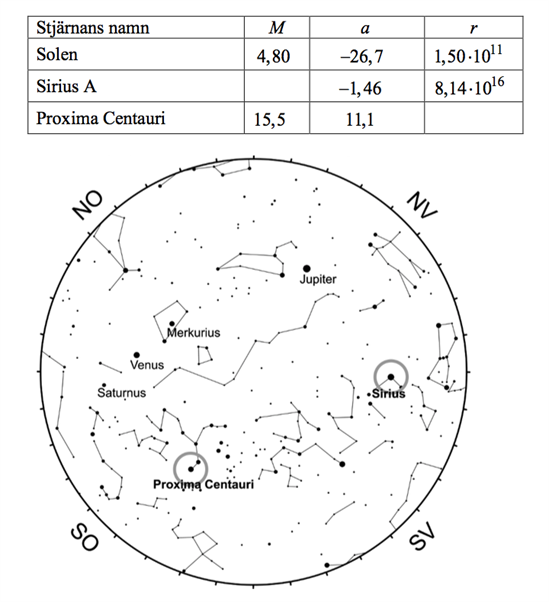
a) Beräkna magnituden M för stjärnan Sirius A.

b) Beräkna avståndet \(r\) till stjärnan Proxima Centauri.

Lösningsförslag

a) För att beräkna magnituden M för stjärnan Sirius A använder vi oss av formeln och informationen som ges i tabellen. Från tabellen kan vi avläsa att för stjärnan Sirius A är: \(a=-1,46\) och \(r=8,14\cdot 10^{16}\). Dessa värden stoppar vi in i formeln och beräknar värdet på M:

$$\begin{align} M-5 &= -1,46-5\lg \left( \frac{8,14\cdot 10^{16}}{3\cdot 10^{16}} \right) \\ M&= -1,46-5\lg \left( \frac{8,14}{3} \right) +5 \end{align}$$

Inskrivning i miniräknaren ger:

$$M \approx 1,37$$

Svar: \(M=1,37\)

b) För att beräkna avståndet \(r\) till stjärnan Proxima Centauri gör vi på ett liknande sätt som i uppgift a). Från tabellen kan vi avläsa att för stjärnan Proxima Centauri är: \(M=15,5\) och \(a=11,1\). Dessa värden stoppar vi in i formeln och beräknar \(r\):

$$\begin{align} 15,5-5 & =11,1-5 \lg \left( \frac{r}{3\cdot 10^{16}} \right) \\ 10,5 &= 11,1-5 \lg \left( \frac{r}{3\cdot 10^{16}} \right) \\ 10,5-11,1 &= -5 \lg \left( \frac{r}{3\cdot 10^{16}} \right) \\ -0,6 &= -5 \lg \left( \frac{r}{3\cdot 10^{16}} \right) \\ 0,12 &= \lg \left( \frac{r}{3\cdot 10^{16}} \right) \\ 10^{0,12} &= 10^{\lg \left( \frac{r}{3\cdot 10^{16}} \right)} \\ 10^{0,12} &= \frac{r}{3\cdot 10^{16}} \\ 3\cdot 10^{16} \cdot 10^{0,12} &= r \\ r &\approx 3,95\cdot 10^{16} \end{align}$$

Svar: \(r=3,95\cdot 10^{16}\)

Uppgiften är hämtad ur "Kursprov Matematik 2c, vårterminen 2015" - Ladda ner provet här.