Normalfördelning

I det förra avsnittet gick vi igenom hur man beräknar standardavvikelsen, vilket är ett mått på spridning kring ett medelvärde. I det här avsnittet ska vi bekanta oss med ett vanligt användningsområde för standardavvikelsen, nämligen normalfördelning.

Vid mätning av många fenomen i naturen och i samhället visar det sig att observationsvärdena tenderar att följa ett visst mönster - en normalfördelning. Det kan röra sig om till exempel längden på vuxna människor, vikten på nyfödda barn, mängden nederbörd som fallit under ett dygn, etc. Observationsvärdena tenderar att huvudsakligen ligga i närheten av värdenas medelvärde, med desto färre observationsvärden som återfinns ju längre från medelvärdet man kommer. Dessa fenomen kan beskrivas med hjälp av en normalfördelningskurva, som kan förväntas se ut ungefär som i figuren nedan när vi har tillräckligt många observationsvärden:

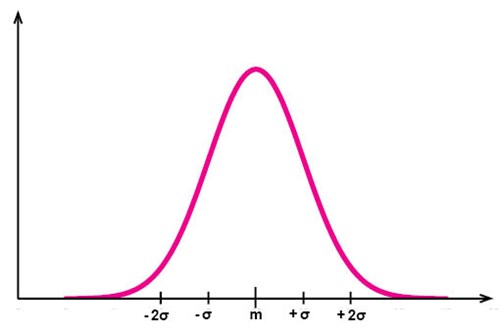
I normalfördelningskurvan i figuren ovan har vi observationsvärden längs x-axeln och värdenas frekvens (hur ofta de förekommer i serien) i y-led.

Vi har också markerat värden på x-axeln som ligger på olika avstånd från medelvärdet. Var dessa markerade värden hamnar beror på standardavvikelsen, vilket vi återkommer till snart.

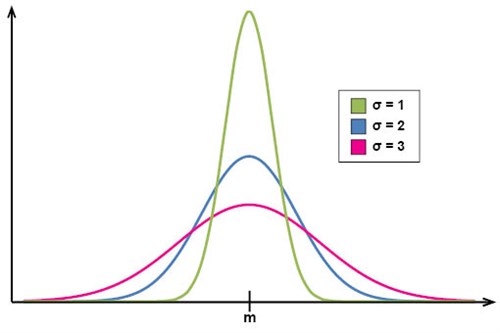
En normalfördelningskurva har alltid formen av en symmetrisk kulle eller puckel. Kurvan ser dock olika ut beroende på medelvärdet, som förskjuter kurvan i x-led, och standardavvikelsen, som ändrar formen på kullen (låg standardavvikelse ger en högre, smalare kulle, medan en hög standardavvikelse ger en lägre, bredare kulle).

I följande figur kan vi se hur olika värden på standardavvikelsen motsvaras av olika utseenden på normalfördelningskurvan. Vid liten standardavvikelse ligger observationsvärdena i allmänhet i närheten av medelvärdet, medan en större standardavvikelse motsvaras av observationsvärden som är mer utspridda relativt medelvärdet:

För alla normalfördelade material gäller att 50 % av observationsvärdena ligger över respektive under medelvärdet (vilket vi kan se på normalfördelningskurvorna genom att kurvan är symmetrisk runt medelvärdet).

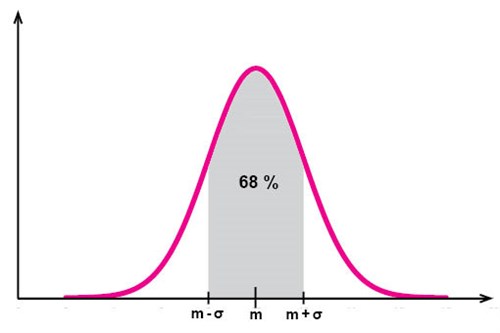
För normalfördelningar gäller också att ungefär 68 % av alla observationsvärden finns inom avståndet en standardavvikelse från medelvärdet:

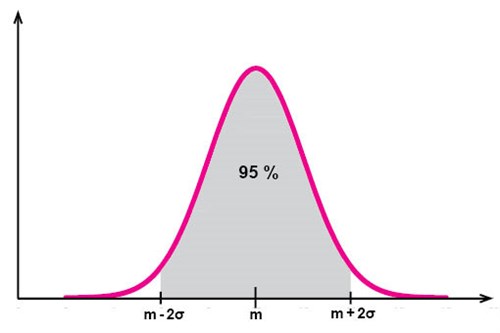
Ungefär 95 % av alla observationsvärden finns inom ett avstånd av två standardavvikelser från medelvärdet:

 Vi tittar på följande exempel

Mellan åren 1966 och 1995 använde man sig i gymnasieskolorna i Sverige (1962-1994 i grundskolan) av det så kallade relativa betygssystemet. Det relativa betygssystemet byggde på föreställningen att kunskapsnivån hos alla som läste samma ämne var normalfördelad och att betygen därför också skulle vara det. Betygen sattes på skalan 1-5 där 7 % av eleverna som läste samma kurs skulle få en 1:a, som var det lägsta betyget, 24 % en 2:a, 38 % en 3:a, 24 % skulle få en 4, och 7 % skulle få en 5:a, vilket var det högsta betyget.

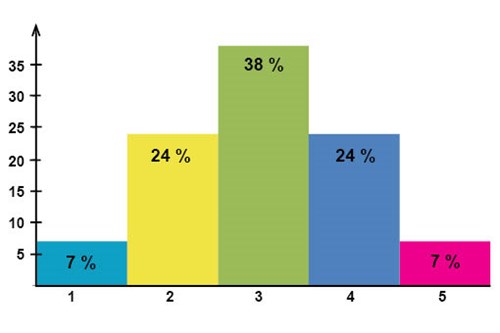
För att kunna jämföra alla elever i hela Sverige som läste samma kurs så införde man centralprov (som var föregångare till dagens nationella prov). De rättades centralt och utifrån resultaten från hela landet kunde betygsgränser sättas. Det relativa betygssystemet fick kritik för att det inte mätte elevernas faktiska kunskap utan bara hur bra de var i förhållande till andra elever. Systemet fick också kritik för att det på många skolor användes på fel sätt, där lärarna "normalfördelade" varje klass. Systemet ersattes 1996 med det mål- och kunskapsrelaterade betygssystemet där det fanns specifika mål för vart och ett av betygsstegen som man måste uppnå för att få ett visst betyg.