Uppgift 14

En cirkel med radien \(a\) tangerar de positiva koordinataxlarna. Den tangerar även en mindre cirkel som har mittpunkten i origo. Se figur.

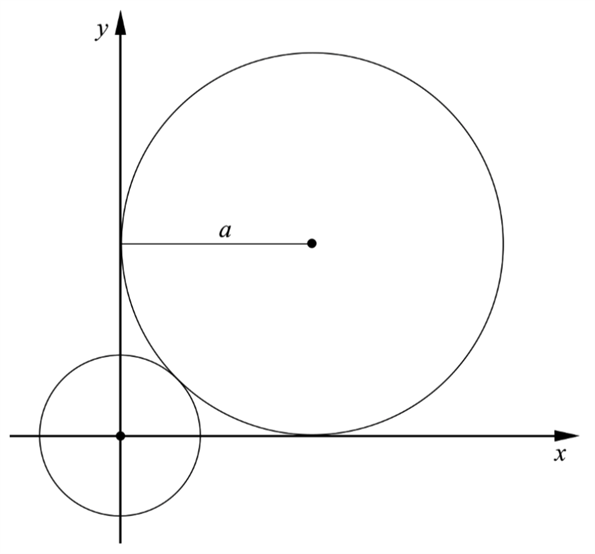
Visa att den mindre cirkelns radie är \(a(\sqrt{2}-1)\) längdenheter.

Lösningsförslag

För att lös uppgiften ritar vi upp följande figur.

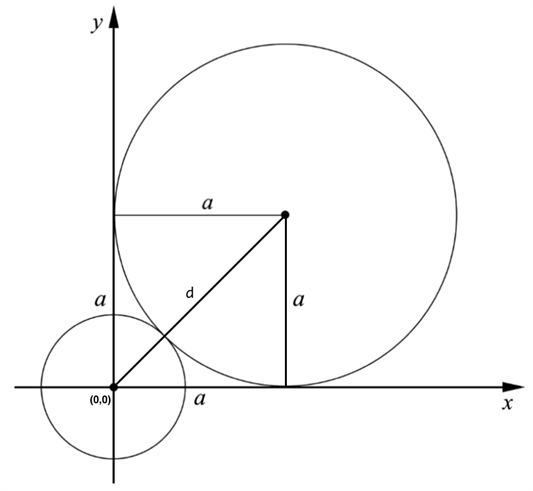
Där fyrkanten är en kvadrat med sidlängderna \(a\) och \(d\) är kvadratens diagonal. För att få fram den lilla cirkelns radie, som vi i denna lösning kallar \(r\), kommer vi att använda Pythagoras sats.

Kvadraten bildar två rätvinkliga trianglar, där sidorna är \(a\) och hypotenusan är \(d\). Den lilla cirkelns radie är \(r=d-a\), eftersom den stora cirkelns radie är \(a\).

För att lösa ut \(d\) använder vi Pythagoras sats som är:

$$a^2+b^2=c^2$$

där \(a\) och \(b\) är sidorna på en rätvinklig triangel och \(c\) är hypotenusan. I vårt fall är båda sidorna \(a\) och hypotenusan \(d\). Vi sätter in det i formeln:

$$\begin{align} a^2+a^2&=d^2 \\2a^2&=d^2 \\ \sqrt{2a^2} & = d \\ d & =a\sqrt{2} \end{align}$$

Eftersom vi i början på lösningen sa att \(r=d-a\) kan vi nu subtrahera \(a\) på båda sidorna för att få fram \(r\):

$$\begin{align} d & =a\sqrt{2} \\ d-a & = a\sqrt{2}-a \\ r &= a(\sqrt{2}-1)\end{align}$$

Svar: Vi har alltså nu visat att den lilla cirkelns radie, \(r\), är

$$r= a(\sqrt{2}-1) \text{  l.e.}$$

VSV

Uppgiften är hämtad ur "Kursprov Matematik 2a, vårterminen 2015" - Ladda ner provet här.