Uppgift 12

Figuren visar två rektanglar som har sidlängderna x respektive (8-x) cm.

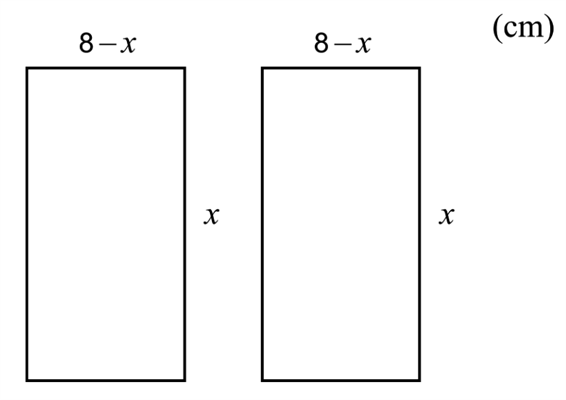
Bestäm den största totala area som de två rektanglarna kan ha tillsammans.

Lösningsförslag

För att lösa denna uppgift behöver vi ställa upp ett uttryck för arean av båda rektanglarna. Sedan tidigare vet vi att arean för en rektangel är: \(A=b\cdot h\). Eftersom vi har två lika stora rektanglar behöver vi multiplicera arean med 2, vilket ger oss formeln:

$$A_{rektanglar}=2\cdot(b\cdot h)$$

Instoppning av bas och höjd ger:

$$\begin{align} A_{rektanglar} & =2\cdot((8-x)\cdot x) \\ & = 2(8x-x^2) \\ & = -2x^2+16x \end{align}$$

Vi kan nu betrakta uttrycket ovan som en andragradsfunktion, där arean är y-värdet. Eftersom vi har en negativ \(x^2\)-term vet vi att funktionen har ett lokalt maximum. För att lösa uppgiften ska vi hitta maximipunktens x-värde och sedan stoppa in den i funktionen för rektanglarnas area, vilket ger oss den största totala area som rektanglarna kan ha.

Vi börjar med att hitta x-värdet till maximipunkten genom att ta fram symmetrilinjen. Vi sätter funktionen \(A_{rektanglar}=0\) och räknar ut funktionens nollställen:

$$\begin{align} 0 & = -2x^2+16x \\ & = -x^2+8x \\ & = x(-x+8) \end{align}$$

Här använder vi oss av nollproduktmetoden för att få fram x-värdena, vilket ger:

$$\begin{align}x_1&=0 \\ x_2&=8\end{align}$$

Symmetrilinjen räknas fram genom följande formeln:

$$x_{symmetri}=\frac{x_1+x_2}{2}$$

Vi får då:

$$x_{symmetri}=\frac{0+8}{2}=4$$

x-värdet för maximipunkten är alltså 4. Insättning i vår funktion ger:

$$\begin{align} A_{rektanglar} &=-2\cdot 4^2 + 16\cdot 4 \\ & = -32+64 \\ & = 32 \end{align}$$

Den största totala arean som båda rektanglarna kan ha tillsammans är alltså \(32 cm^2\).

Svar: \(32cm^2\)

Uppgiften är hämtad ur "Kursprov Matematik 2b, vårterminen 2015" - Ladda ner provet här.