Uppgift 25

Ett företag tillverkar anslagstavlor av olika storlekar. Varje anslagstavla består av en rektangulär platta omgiven av en ram. Ramen består av fyra delar som sågas till av en 5 cm bred trälist. Delarnas ändar är sågade med vinkeln 45^o och trälistens utseende gör att delarna bara kan monteras på ett sätt. Ramen monteras så att den går 2 cm in över plattans framsida. Se figur.

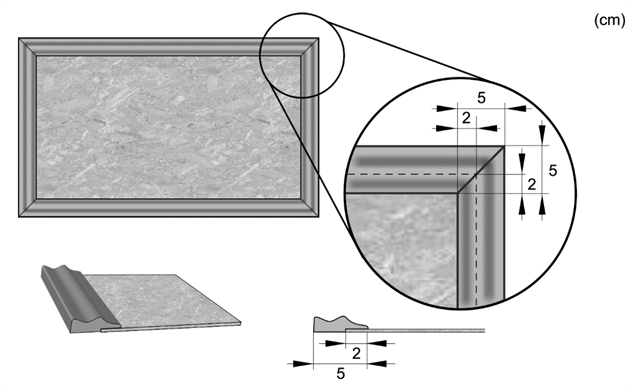
Materialkostnaden för en anslagstavla beror på plattans area och trälistens längd. Priset för plattan anges i kr/m² och trälisten i kr/m.

Materialkostnaden för en anslagstavla med bredden 36 cm och längden 46 cm är 59 kr. För en anslagstavla med bredden 46 cm och längden 56 cm är materialkostnaden 81 kr. Se figur.

Teckna ett generellt uttryck för den totala materialkostnaden för anslagstavlor som har bredden \(a\) m och längden \(b\) m.

Lösningsförslag

Vi börjar med att lösa ut kostnaderna för pris av plattan och pris för trälisten. Vi tällsätter två variabler:

\(x\)=kr/m², pris för plattan
\(y\)=kr/m, pris för trälisten

Vi börjar med att titta på den vänstra anslagstavlan i figuren för att ställa upp en ekvation för kostnaden.

Längden på trälisten är \(2\cdot(36cm+46cm)=2\cdot82cm=164cm=1,64m\)

Arean på plattan är beräknas genom att först ta reda på längden av plattans sidor och sedan multiplicera dem.

Längden på plattans sidor är \(36cm-6cm=30cm=0,3m\) och \(46cm-6cm=40cm=0,4m\).

Arean på plattan är då \(0,3m \cdot 0,4m=0,12m^2\)

Ekvationen för kostnaden blir alltså:

$$0,12x+1,64y=59$$

Gör vi samma utträkning för den högra anslagstavlan i figuren får vi följande ekvation:

$$0,2x+2,04y=81$$

Tillsammans ger det ekvationssystemet:

$$\begin{cases} 0,12x+1,64y=59 \\ 0,2x+2,04y=81\end{cases}$$

För att lösa ekvationen använder vi oss av additionsmetoden, men först måste vi se till att variablerna för antingen x eller y har samma koefficient, fast med olika tecken. Om vi multiplicerar ekvation 2 med 0,6 så kommer koefficienterna för x-variabeln båda vara 0,12. Eftersom de ska ha olika tecken måste vi multiplicera med -0,6. Vilket ger det nya ekvationssystemet:

$$\begin{cases} 0,12x+1,64y=59 \\ -0,12x-1,224y=-48,6 \end{cases}$$

Addition av ekvationerna ger:

$$\begin{align} 0,416y&=10,4 \\ y&=25 \end{align}$$

Insättning i den första ekvationen ger:

$$\begin{align} 0,12x+1,64\cdot25&=59\\ 0,12x+41 &=59\\ 0,12x &=18 \\ x&=150\end{align}$$

Vi har nu fått fram priserna för plattan och trälisterna:

\(x=150\) kr/m², pris för plattan
\(y=25\) kr/m, pris för trälisten

Kvar är att teckna ett generellt uttryck för den totala materialkostnaden för anslagstavlorna som har bredden \(a\) m och längden \(b\) m.

Den generella arean för plattan är \((a-0.06)(b-0,06)=ab-0,06a-0,06b+0,0036\) m².

Den genrella längen på trälisterna är \(2(a+b)=2a+2b\) m.

Vi multiplecerar uttycken med kostnaden och adderar ihop dem för att få det generella uttrycket:

$$\begin{align} &(ab-0,06a-0,06b+0,0036)\cdot150+(2a+2b)\cdot25 \\ &= 150ab-9a-9b+0,54+50a+50b \\ &= 150ab+41a+41b+0,54 \end{align}$$

Svar: Det generella uttrycket för den totala materialkostnaden är \(150ab+41a+41b+0,54\).

Uppgiften är hämtad ur "Kursprov Matematik 2c, vårterminen 2015" - Ladda ner provet här.