Uppgift 13
Thales från Miletos var en grekisk matematiker som levde för 2600 år sedan.
Han formulerade en sats med följande innebörd:
Varje triangel som är inskriven i en cirkel har en rät vinkel om en av triangelns
sidor är diameter i cirkeln.
Triangeln ABC är inskriven i en cirkel på ett sådant sätt. Sidan AC är en diameter i cirkeln. Punkten M är mittpunkt på sträckan AC. I figuren är även sträckan BM inritad.
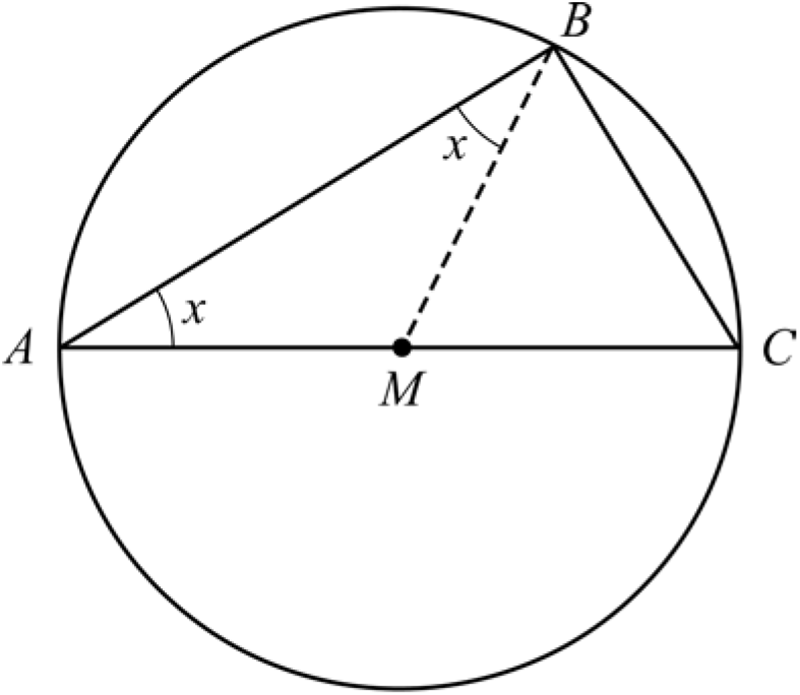
- Förklara varför de två vinklarna betecknade med x är lika stora.
- Visa, utan att använda randvinkelsatsen, att Thales sats är korrekt.
Rättelse! Trianglarna AMB och BMC är likbenta, inte liksidiga som det sägs i videon.
a) T.ex. "Triangeln ABM är likbent för att AM och BM är radier i cirkeln."
b) Se videolektion
Uppgiften är hämtad ur "Kursprov Matematik 2c, vårterminen 2012" - Ladda ner provet här
