Randvinkelsatsen

Innan vi går in på den sats som vi ska behandla i det här avsnittet, ska vi börja med att gå igenom några viktiga begrepp.

Definitioner

Vi utgår från en cirkel enligt figuren nedan.

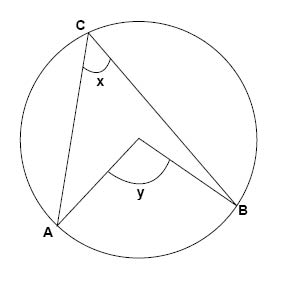
I denna figur ovan har vi en medelpunkt i mitten av cirkeln. Vi har också två punkter A och B som ligger på cirkelns rand, det vill säga som ligger på en radies avstånd från cirkelns medelpunkt. Dessa båda punkter bildar en cirkelbåge AB. Vi har också en tredje punkt C, som också ligger på cirkelns rand. En sträcka såsom AC och BC i figuren, alltså sträckan mellan två punkter en cirkel, kallas en korda.

Utöver detta har vi två intressanta vinklar: vinkeln y, som är medelpunktsvinkeln till cirkelbågen AB, och vinkeln x, som är den randvinkel som bildas då punkten C med hjälp av kordor sammanbinds med punkterna A och B enligt figuren.

Randvinkelsatsen

Randvinkelsatsen anger att medelpunktsvinkeln (y) till cirkelbågen AB är dubbelt så stor som randvinkeln (x) som står på samma cirkelbåge AB, alltså att

$$y=2x$$

Följdsatser

Av randvinkelsatsen får vi några följdsatser:

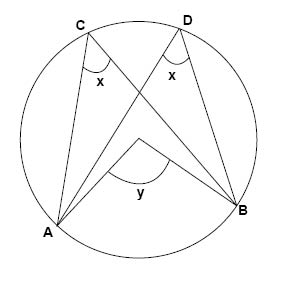
Alla randvinklar till samma cirkelbåge är lika stora, eftersom randvinkelsatsen säger att randvinkeln är hälften så stor som medelpunktsvinkeln på samma cirkelbåge och eftersom alla randvinklarna ligger på samma cirkelbåge kommer de alla vara hälften så stora som medelpunktsvinkeln.

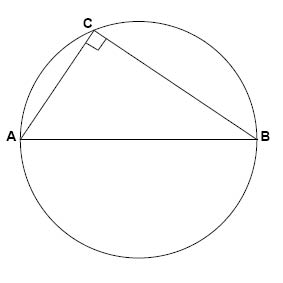
Randvinklar till en halvcirkelbåge är 90°, eftersom ett halvt varv är 180°. Detta kallas också för Thales sats.

Skriver vi in en fyrhörning i en cirkel så kommer vinkelsumman av motstående vinklar alltid  vara 180°.

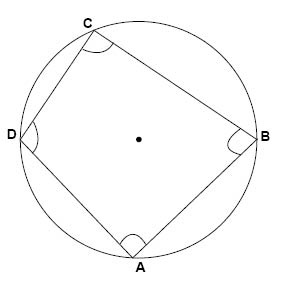
$$\measuredangle A+\measuredangle C=180^{\circ}$$

$$\measuredangle B+\measuredangle D=180^{\circ}$$

Bevis för randvinkelsatsen

Här nedan följer ett bevis för randvinkelsatsen.

För att bevisa randvinkelsatsen börjar vi med att rita en diameter som går mellan de båda vinklarnas vinkelspetsar. Diametern kommer då att dela de båda vinklarna x och y i två vinklar vardera, vinklar som vi betecknar x1 och x2, respektive y1 och y2.

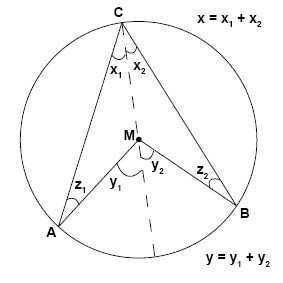
Vinklarna y1 och y2 är yttervinklar till \(\triangle AMC\) och \(\triangle BMC\), och yttervinkelsatsen ger då att:

$$y_{1}=x_{1}+z_{1}\;\;och\;\;y_{2}=x_{2}+z_{2}$$

Eftersom trianglarna ACM och BCM båda är likbenta (sidorna AM, CM och BM är alla samma som cirkelns radie) så är

$$x_{1}=z_{1}\;\;och\;\;x_{2}=z_{2}$$

Vilket gör att

$$y_{1}=x_{1}+x_{1}=2x_{1}\;\;och\;\;y_{2}=x_{2}+x_{2}=2x_{2}$$

$$y_{1}+y_{2}=2x_{1}+2x_{2}=2(x_{1}+x_{2})$$

$$y=2x$$

V.S.B.

---

Videolektioner

Här går vi igenom randvinkelsatsen.

 

Bevis för randvinkelsatsen för ett av tre möjliga fall.

Följdsatser av randvinkelsatsen.