Uppgift 9
ABC är en triangel. Vad är x + z?
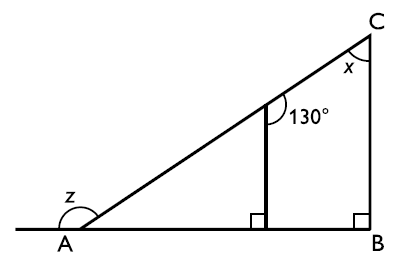
A 130°
B 140°
C 180°
D 190°
Lösningsförslag:
Det finns många sätt att lösa uppgiften på men en bra utgångspunkt är att gå igenom vad vi vet om trianglar i allmänhet och vad som är specifikt för triangeln ABC.
Till att börja med ser vi att triangeln är rätvinklig eftersom vinkeln B är 90° (markeras med en kvadrat istället för en vinkelbåge) och att x = vinkeln C.
Den stora triangeln och den lilla triangeln är likformiga eftersom de båda är rätvinkliga och de har vinkeln A gemensam. Det betyder att den övre vinkeln i den lilla triangeln är lika med x. Eftersom ett halvt varv är lika med 180° så är den övre vinkeln i den lilla triangeln lika med 180° - 130° = 50°. Eftersom vi redan konstaterat att den vinkeln är lika med x får vi att x = 50°.
Allmänt gäller att vinkelsumman i en triangel alltid är lika med 180°, vilket betyder att A + B + C = 180°. Vi vet att B = 90° och C = 50°, vilket ger
$$A+90°+50°=180°$$
$$A=180°-90°-50°$$
$$A=40°$$
Vi använder återigen sambandet att ett halvt varv är lika med 180° vilket betyder att A + z = 180°. Eftersom A = 40° är z = 180° - 40° = 140°. Vi vill veta vad x + z är:
$$x+z=50°+140°=190°$$
Rätt svar är därför alternativ D (190°)
