Uppgift 12

Ladda ner provet från Mattebokens provbank här.

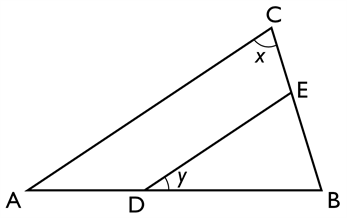
ABC är en triangel. DE är parallell med AC, och DE=BD. Vad är x?

A. $90^\circ - 2y$
B. $180^\circ - y$
C. $90^\circ - \frac{y}{2}$
D. $\frac{180^\circ - 2y}{2}$

Lösningsförslag

För att lösa denna uppgift kommer vi använda våra kunskaper om trianglar och likformighet.

Informationen att DE = BD medför att triangeln BED är likbent. Alltså är vinklarna $\angle DEB$ och $\angle DBE$ är lika stora.

Vidare vet vi att sträckorna DE och AC är parallella. När sträckor i trianglar är parallella och skärs av samma räta linjer kommer de vinklar som uppstår alltid att vara identiska. Alltså:

$\angle CAB=\angle EDB =y$
$\angle ACB =\angle DEB = x$

Triangeln ABC har alltså en vinkel $\angle CAB = y$ och två vinklar $\angle ACB = \angle ABC = x$. Vinkelsumman i en triangel är alltid lika med $180^\circ$, därför kan triangelns vinkelsumma skrivas med ekvationen $y+2x=180^\circ$. Genom att lösa ut $x$ får vi det sökta svaret:

$$\begin{align} y+2x & =180\\ 2x &= 180-y \\ x &= \frac{180-y}{2} \\ x &= 90- \frac{y}{2} \end{align}$$

Alltså har vi fått fram att $x=90^\circ- \frac{y}{2}$, vilket är C.

Svar: C

Uppgiften är hämtad ur Högskoleprovets kvantitativa del höstterminen 2017, Provpass 3 - Ladda ner provet här.