Provpass 5 - XYZ

Matematisk problemlösning - XYZ

1. (4x + 13 = 8x - 31)
Vad är x?

-4,5
1,5
4,5
11

$8x-4x =13+31$ $4x=44$ $x=\frac{44}{4}=11$ Svar: D

2. Vilken av punkterna ligger på linjen L?

(-5, 1)
(-3, -2)
(1, -5)
(3, -3)

Sätt in alla punkter och kolla om någon ligger på linjen. A (-5,1) ligger ej på linjen, B (-3,-2) ligger ej på linjen, C (1,-5) ligger på linjen, D (3,-3) ligger ej på linjen

Svar: C

3. Vad är $\frac{1}{3} - (\frac{1}{2} + \frac{1}{6})$ ?

$-\frac{2}{3}$
$-\frac{1}{3}$
0
$\frac{1}{3}$

$\frac{1}{3} - \left(\frac{1}{2} + \frac{1}{6}\right)=\frac{2}{6} - \left(\frac{3}{6} + \frac{1}{6}\right)=\frac{2}{6} - \frac{4}{6}=- \frac{2}{6}=- \frac{1}{3}$ Svar: B

4. Medelvärdet av 17, 21 och 44 är lika med medelvärdet av 63, 73 och x.
Vilket värde har x?

Medelvärde av 17, 21 och 44 är (17+21+44)/3 =82/3
$\Rightarrow \frac{63+73+x}{3}=\frac{82}{3}$ $\Rightarrow 63+73+x=82 \Rightarrow136+x=82$ $x=-54$ Svar: A

5. Vägen mellan Julias hem och Annas hem är 12 km lång. De startar hemifrån samtidigt för att mötas längs vägen. Julia springer med konstant hastighet och det tar henne 12 minuter att springa 2 km. Anna går med konstant hastighet och det tar henne 24 minuter att gå 2 km. Hur lång tid tar det innan de möts?

36 minuter
42 minuter
48 minuter
72 minuter

Julias hastighet = 2 km/12 min = 1/6 km/min
Annas hastighet = 2 km/24 min = 1/12 km/min

Tiden då de möts är t. Då har Julia hunnit $s$ km och Anna har hunnit ( $12-s$ ) km

$\frac{1}{6}\cdot t =s$ $\frac{1}{12}\cdot t = 12-s$ $s=12-\frac{1}{12}\cdot t$ $12-\frac{1}{12}\cdot t=\frac{1}{6}\cdot t$
$12= \frac{2}{12}\cdot t + \frac{1}{12}\cdot t=\frac{3}{12}\cdot t$ $12=\frac{3}{12}\cdot t$ $12=\frac{1}{4}\cdot t$ $t=48$ Alternativt lösningsförslag (resonerande)
På 24 minuter har Anna hunnit 2 km och Julia 4 km. Efter ytterligare 24 min har Anna totalt gått 4 km och Julia totalt 8 km. Då möts de.

Svar: C

6. Vilket av svarsalternativen är lika med 7?

$\sqrt{29}+\sqrt{20}$
$7^1+7^0$
$\frac{14}{7}+\frac{49}{14}$
$\left(\frac{7}{\sqrt{7}}\right)^2$

$\left(\frac{7}{\sqrt{7}}\right)^2=\frac{\left(7\right)^2}{\left(\sqrt{7}\right)^2}=\frac{7\cdot 7}{7}=7$ Svar: D

7. Vilket svarsalternativ är lika med 18 procent av $\frac{2}{5}$ ?

$\frac{1}{45}$
$\frac{4}{45}$
$\frac{9}{125}$
$\frac{9}{250}$

$18\% = \frac{18}{100}$ Beräkna $\frac{2}{5}\cdot \frac{18}{100}$

Förkorta 2 mot 100 $\frac{2}{5}\cdot \frac{18}{100}=\frac{1}{5}\cdot \frac{18}{50}=\frac{1}{5}\cdot \frac{9}{25}= \frac{9}{125}$ Svar: C

8. A, B och C är tre av hörnen i en kvadrat med sidlängden 4 cm. Kvadratens fjärde hörn, M, är medelpunkten för en cirkel med radien 2 cm. Hur stor är arean av det skuggade området i figuren?

$\left(12+\frac{\pi}{2}\right)\;cm^2$
$\left(12+\frac{\pi}{4}\right)\;cm^2$
$\left(16-\frac{\pi}{2}\right)\;cm^2$
$\left(16-\pi \right)\;cm^2$

Yta kvadrat $= 4\cdot 4=16$ ; Yta kvarts cirkel $=\frac{\pi \cdot 2^2}{4}=\pi$ . Yta grått område är $16-\pi$

Svar: D

9. Vilket svarsalternativ är en ekvation för en linje som går genom punkten (3, 1)?

y = -x + 4
y = x + 2
y = 2x + 1
y = 3x + 1

Sätt in punkten (3, 1) i ekvationerna dvs $x=3$ och $y=1$ ; $A: y=-x+4 \Rightarrow 1=-3+4=1$ . A är rätt.

Svar: A

10. a, b och c är positiva tal sådana att $\frac{a}{b}=\frac{b}{c}$ och $c=2a$ . Vad är b uttryckt i a?

$b=a\sqrt{2}$
$b=\frac{a}{\sqrt{2}}$
$b=2\sqrt{a}$
$b=\frac{\sqrt{a}}{2}$

Sätt in $c=2a$ i uttrycket $\Rightarrow \frac{a}{b}=\frac{b}{2a} \Rightarrow 2a^2=b^2 \Rightarrow b=a\sqrt{2}$ Svar: A

11. $x\cdot 10^4 - 2x \cdot 10^3 = 3,2 \cdot 10^4$

Vilket värde har x?

Förkorta $10^3$ ur uttrycket $10x-2x=3,2\cdot 10 \Rightarrow 8x=32 \Rightarrow x=4$ Svar: A

12. Kvadraterna $K_1$ och $K_2$ överlappar varandra så att 25 procent av arean av $K_1$ täcks av 20 procent av arean av $K_2$ . Kvadraten $K_1$ har sidlängden 2 cm. Vilken sidlängd har $K_2$ ?

1,6 cm
$\sqrt{3}$ cm
$\sqrt{5}$ cm
2,5 cm

Rita kvadraterna lite överlappande:

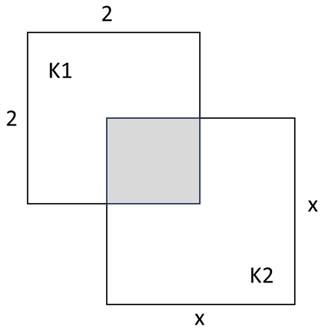
hp 24 provpass 5 xyz uppgift 12

$25\%$ av $K_1$ : yta $= 0,25\cdot 4$

$20\%$ av $K_2$ : yta $= 0,2\cdot x^2$

$25\%$ av $K_1$ = $20\%$ av $K_2$ $\Rightarrow 1=0,2\cdot x^2 \Rightarrow x^2=5 \Rightarrow x=\sqrt{5}$ Svar: C

Har du en fråga du vill ställa om Provpass 5 - XYZ? Ställ den på Pluggakuten.se

Har du hittat ett fel, eller har du kommentarer till materialet på den här sidan? Mejla matteboken@mattecentrum.se