Uppgift 14

Kvantitet I: Diagonalen i rektangeln ABCD

Kvantitet II: Halva omkretsen i rektangeln ABCD

A   I är större än II 
B   II är större än I 
C   I är lika med II 
D   informationen är otillräcklig

---

När vi ska lösa den här uppgiften är det en bra idé att börja med att skissa upp en rektangel ABCD och markera diagonalen.

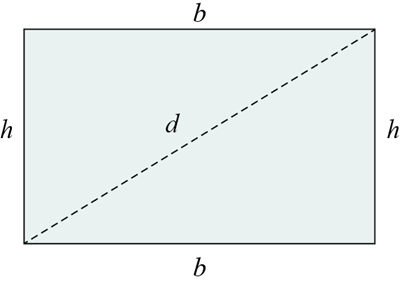
Eftersom en rektangels omkrets är summan av längden av dess sidor, kommer halva omkretsen att vara hälften av denna summa.

En rektangel omkrets skriver vi så här:

$$O=2\cdot b+2\cdot h$$

där b är rektangelns bas och h är dess höjd.

Halva omkretsen är därför följande:

$$\frac{O}{2}=\frac{2\cdot b+2\cdot h}{2}=b+h$$

Det här innebär att vi kan se uppgiften som att vi ska jämföra vilket som är störst, längden av en rätvinklig triangels hypotenusa eller summan av triangelns kateter.

I en rätvinklig triangel kommer längden av hypotenusan alltid att vara mindre än summan av längden av kateterna, så halva omkretsen i rektangeln ABCD kommer alltid att vara större än diagonalen i den rektangeln.

Rätt svarsalternativ är därför B (II är större än I).