Uppgift 1
Hur stor är vinkeln v?
A 92°
B 97°
C 103°
D 105°
Vi löser den här uppgiften genom att använda kunskapen om att vinkelsumman i trianglar alltid är 180°.
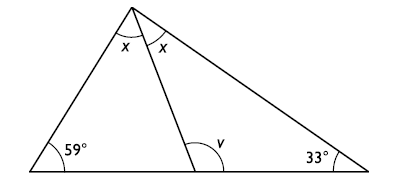
Den stora triangeln som visas i figuren har tre vinklar: en vinkel som är 59°, en vinkel som är 33° och en vinkel som är 2x. Eftersom vinkelsumman i denna triangel måste vara 180° kan vi teckna följande ekvation:
$${59}^{\circ}+{33}^{\circ}+2x={180}^{\circ}$$
Om vi löser denna ekvation så får vi reda på hur stor vinkeln x är. Denna information kan vi sedan använda för att ta reda på hur stor vinkeln v är, vilket ju är vad uppgiften går ut på.
Vi löser ekvationen:
$$2x={180}^{\circ}-{59}^{\circ}-{33}^{\circ}={88}^{\circ}$$
$$x={88}^{\circ}/2={44}^{\circ}$$
Nu vet vi alltså att vinkel x är 44°.
Vi använder ännu en gång vinkelsumman för trianglar för att teckna en ekvation utifrån den triangel som vinkeln v ingår i:
$$v+x+{33}^{\circ}={180}^{\circ}$$
Vi löser ut v ur denna ekvation och sätter in x = 44°.
$$v={180}^{\circ}-x-{33}^{\circ}=$$
$$={180}^{\circ}-{44}^{\circ}-{33}^{\circ}={103}^{\circ}$$
Nu har vi alltså kommit fram till att vinkeln v måste vara 103°.
Rätt svarsalternativ är därför C (103°).
