Uppgift 19

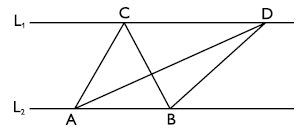
L$_1$ och L$_2$ är parallella linjer. A, B, C och D är punkter på dessa linjer.
AD är längre än AC.

Kvantitet I: Arean av triangeln ABC

Kvantitet II: Arean av triangeln ABD

A   I är större än II 
B   II är större än I 
C   I är lika med II 
D   informationen är otillräcklig

---

 

I den här uppgiften ska vi jämföra två trianglars area. Därför måste vi känna till formeln som vi använder när vi beräknar en triangels area:

$${A}_{triangel}=\frac{b\cdot h}{2}$$

Det som eventuellt kan vara svårt i uppgiften är att se vad basen b och höjden h är för de två trianglarna.

För triangeln ABC gäller att basen b är avståndet mellan punkterna A och B. Höjden h är avståndet mellan de två parallella linjerna L₁ och L₂. Om vi betecknar avståndet mellan punkterna A och B med |AB|, så får följande area för triangeln ABC:

$${A}_{{}_{ABC}}=\frac{|AB|\cdot h}{2}$$

Även triangeln ABD har en bas b som utgörs av avståndet mellan punkterna A och B. Höjden h är avståndet mellan linjerna L₁ och L₂. Använder vi samma beteckningar som ovan, får vi därför följande area för triangeln ABD:

$${A}_{{}_{ABD}}=\frac{|AB|\cdot h}{2}$$

Som vi nu ser gäller

$${A}_{{}_{ABC}}={A}_{{}_{ABD}}$$

så kvantitet I är lika med kvantitet II.

Rätt svarsalternativ är därför C (I är lika med II).