Kvantitativa jämförelser
13.
Kvantitet I: \(4 \% \text{ av } 200\)
Kvantitet II: En fjärdedel av \(20\)
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Kvantitet I: \(\frac{4}{100} \cdot 200 = \frac{800}{100} = 8\)
Kvantitet II: \(\frac{1}{4} \cdot 20 = \frac{20}{4} = 5\)
Svar: A
14.

Kvantitet I: \(x+y+z+w\)
Kvantitet II: \(360^\circ\)
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
\(x\), \(y\), \(z\) och \(w\) är vertikalvinklar med fyrhörningens vinklar. Vinkelsumman i en fyrhörning är \(360^\circ\) (om man ritar en diagonal får man 2 trianglar; summan på fyrhörningens vinklar blir summan på båda trianglarnas vinklar, alltså \(2 \cdot 360^\circ = 360^\circ\)).
Svar: C
15. \(f(x) = 10 - 3x\)
- Kvantitet I: \(f(2)-f(5)\)
- Kvantitet II: \(f(0)-f(4)\)
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Kvantitet I:
$$f(2) = 10 - 3 \cdot 2 = 10 - 6 = 4$$
$$f(5) = 10 - 3 \cdot 5 = 10 - 15 = -5$$
$$f(2) - f(5) = 4 - (-5) = 4 + 5 = 9$$
Kvantitet II:
$$f(0) = 10 - 3 \cdot 0 = 10 - 0 = 10$$
$$f(4) = 10 - 3 \cdot 4 = 10 - 12 = -2$$
$$f(0) - f(4) = 10 - (-2) = 10 + 2 = 12$$
Svar: B
16.
- Kvantitet I: \(\frac{1}{5}+\frac{1}{10}+\frac{1}{15}\)
- Kvantitet II: \(\frac{1}{3}\)
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Kvantitet I:
\( \begin{align*} \frac{2}{10}+\frac{1}{10}+\frac{1}{15}
&=\frac{3}{10}+\frac{1}{15}\\ &=\frac{3\cdot3}{10\cdot3}+\frac{1\cdot2}{15\cdot2} \\ &=
\frac{9}{30}+\frac{2}{30} \\ &=\frac{11}{30} \end{align*} \)
Kvantitet II:
\(\frac{1}{3}=\frac{1\cdot10}{3\cdot10}=\frac{10}{30}\)
Svar: A
17. \(\frac{x}{16}=\frac{3}{12x}\)
- Kvantitet I: \(x\)
- Kvantitet II: \(4\)
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Förkorta HL med 3: \(\frac{x}{16}=\frac{1}{4x}\)
Multiplicera båda led med \(4x\): \(\frac{x}{16}\cdot 4x=\frac{1}{4x}\cdot 4x\)
\(\frac{4x^2}{16}=1\)
\(\frac{x^2}{4}=1\)
\(x^2=4\)
\(x=\pm 2\)
Svar: B
18.

- Kvantitet I: Omkretsen av sexhörningen ABCDEF
- Kvantitet II: 24 cm
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Vi får lägga till EH och CH som parallella med DC och DE, då vet vi ED=HC och EH=HC.
Så omkretsen av sexhörningen ABCDEF är lika med omkretsen av rektangeln ABHF.
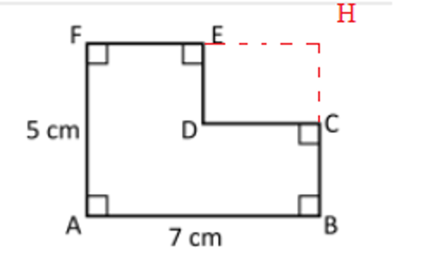
Så Kvantitet I \(= 2\cdot(5+7)= 24\) cm = Kvantitet II.
Svar: C
19.
\(x<0\)
\(y<1\)
- Kvantitet I: \(x^2\)
- Kvantitet II: \(x^2y\)
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
\(x<0\) och \(y<1\), så Kvantitet I > 0,
Om \(y\leq 0\), då Kvantitet II \(\leq 0\), då \(x^2> x^2y\)
Om \(0<y<1\), så \(x^2>x^2y\).
Svar: A
20. En burk innehåller endast enfärgade röda och svarta kulor. Antalet svarta kulor är fem gånger så stort som antalet röda kulor.
- Kvantitet I: Sannolikheten att en slumpmässigt vald kula ur burken är röd
- Kvantitet II: 1/5
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Om antalet röda kulor är \(x\), då antalet svarta kulor är \(5x\).
Så Kvantitet I är \(\frac{x}{x+5x}=\frac{1}{6}\)
Kvantitet II är \(\frac{1}{5}\)
Så Kvantitet I < Kvantitet II
Svar: B
21. \(x\) och \(y\) är heltal sådana att
\(16<x<25\)
\(16<y<25\)
\(x\) är inte jämnt delbart med vare sig 3 eller 5.
\(y\) är jämnt delbart med 2.
- Kvantitet I: Antalet olika tal som x kan vara
- Kvantitet II: Antalet olika tal som y kan vara
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
\(E= {17,18,19,20,21,21,23,24}\)
Siffrorna inte jämnt delbart med vare sig 3 eller 5 är {17,19,22,23}, då Kvantitet I = 4
Siffrorna jämnt delbart med 2 är{18,20,22,24}, då Kvantitet II =4
Så Kvantitet I = Kvantitet II
Svar: C
22. \(\sqrt{5}\cdot \sqrt{9}=45^x\)
- Kvantitet I: \(x\)
- Kvantitet II: \(0,5\)
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
\(\sqrt{5}\cdot \sqrt{9}=\sqrt{45}\), są vi kań skriva att
\(\sqrt{45}=45^x\), dvs. \(45^{\frac{1}{2}}=45^x\)
Så \(x=\frac{1}{2}=0,5\)
Alltså Kvantitet I = Kvantitet II
Svar: C
