Provpass 5 - KVA
Kvantitativa jämförelser - KVA
13. 3x > y
- Kvantitet I: x
- Kvantitet II: y
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Det finns ingen information om värden på x och y, så informationen är otillräcklig.
Man kan ganska lätt hitta värden som uppfyller A och B:
x = 1, y = 2 respektive x = 100, y = 2
Svar: D
14. H är en regelbunden sexhörning.

- Kvantitet I: Andelen av H som är skuggad
- Kvantitet II: Andelen av H som inte är skuggad
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
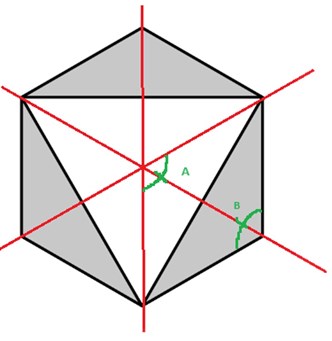
Innervinklar i en hexagon är 120 grader, eftersom vinkelsumman är 720 grader (\(=180\cdot 4\), fyra inskrivna trianglar).
Drar man diagonaler bildas sex innervinklar i centrum. Vinkelsumman av dessa är 360 grader, ett helt varv. Två sådana vinklar bildar 120 grader.
Detta ger vinkel A = vinkel B. Det ger att ytorna/trianglarna som respektive vinkel “spänner upp” måste vara lika eftersom de delar motstående sida.
Alltså måste de vita trianglarna tillsammans utgöra samma area som de skuggade.
Svar: C
15. \(2(x-4)=\frac{1}{2}\)
- Kvantitet I: x
- Kvantitet II: 5
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
$$2(x-4)=\frac{1}{2}$$ $$(x-4)=\frac{1}{4}$$ $$x=\frac{1}{4}+4=\frac{17}{4}=4,25$$ $$5 > 4,25$$ Svar: B
16. f(x) = 4x + 8
g(x) = 2x + 4
- Kvantitet I: f(a)
- Kvantitet II: g(2a)
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
$$f(a)=4a+8$$ $$g(2a)=2\cdot 2a+4=4a+4$$
$$4a+8 > 4a+4\; \text{för}\; a>0$$ Svar: A
17. En mätserie består av tio heltal mellan 1 och 50. Mätseriens median är 25.
- Kvantitet I: Mätseriens median om det största och det minsta mätvärdet tas bort
- Kvantitet II: 25
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Medianväde definieras som värdet mitt i serien. Om det initialt är 25 och man sedan tar bort det största respektive minsta, så förändras inte vilket värde som är mitt i serien.
Exempel:
1, 5, 10, 15, 20, 30, 35, 40, 42, 50
Median: 25
_, 5, 10, 15, 20, 30, 35, 40, 42, __
Median 25
Svar: C
18. Kvantitet I: \(4\cdot 10^{-2}\)
- Kvantitet II: \(\frac{1}{400}\)
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
$$4\cdot 10^{-2} = 0,04$$ $$\frac{1}{400} = \frac{1}{4} \cdot \frac{1}{100} = \frac{1}{4} \cdot 10^{-2} = 0,0025$$ $$0,04 > 0,0025$$ Svar: A
19. \(-1 <x<0\)
\(0<y<1\)
- Kvantitet I: \(\frac{y}{x}\)
- Kvantitet II: \(\frac{x}{y}\)
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Titta på skillnaden mellan kvantiteterna.
$$\frac{y}{x}-\frac{x}{y}=\frac{y^2}{xy}-\frac{x^2}{xy}=\frac{y^2-x^2}{xy}$$
Nämnaren (xy) är alltid negativ eftersom \(x<0\) och \(y>0\). Täljaren \(y^2-x^2\) kan vara både positiv och negativ beroende på värden på x och y.
Skillnaden kan alltså både vara positiv och negativ. Informationen är således otillräcklig.
Svar: D
20. Fyrhörningen ABCD är en kvadrat. De två parallella linjerna \(L_1\) och \(L_2\) går genom punkten C respektive punkten A.

- Kvantitet I: \(20^\circ\)
- Kvantitet II: \(x-50^\circ\)
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
AB är parallell med CD, så vinkeln mellan AB och linjen \(L_2\) är 20°. Vinkel BAD är 90° (rät). Tillsammans med vinkeln \(x\) är dessa 180° (ett halvt varv): $$x + 20° + 90° = 180°$$ $$x = 70°$$ Kvantitet II \(= x - 50° = 20° =\) Kvantitet I
Svar: C
21. \(x<0\)
- Kvantitet I: \((x+4)(x-2)\)
- Kvantitet II: \((x-4)(x+2)\)
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Expandera parenteserna. $$Kvantitet\; I\; = x^2+2x-8$$ $$Kvantitet\; II\; = x^2-2x-8$$ Skillnaden mellan kvantitet I och II är:
Kvantitet I - Kvantitet II \(= 2x - (-2x) = 4x\)
Eftersom \(x<0\) så är skillnaden alltid negativ, så Kvantitet II är större än Kvantitet I.
Svar: B
22. Priset på en vara stiger med \(20\%\) per år.
- Kvantitet I: Den tid det tar tills priset har fördubblats
- Kvantitet II: 5 år
- I är större än II
- II är större än I
- I är lika med II
- informationen är otillräcklig
Efter 1 år är priset 1,2 ggr högre.
Efter 2 år är priset \(1,2\cdot 1,2 = 1,44\) ggr högre
Efter 4 år är priset \(1,44\cdot 1,44 = 2,0736\) ggr högre
Priset har alltså mer än fördubblats på 4 år.
Svar: B
