Diagram, tabeller och kartor

Identifiera kolumnen för garantipension (längst till höger), och markera det totala antalet pensionärer med garantipension, samt det totala antalet kvinnliga pensionärer med garantipension: Siffrorna kan avrundas till 520 000 och 660 000 inledningsvis. Detta ger oss andelen:  \(\frac{52\,000}{66\,000}\)

Vilket kan förenklas till \(\frac{52}{66}\). Vidare förenkling (båda tal är delbara med två) ger oss \(26/33\). Här kan vi notera att nämnaren är 33, och att \(33\cdot 3\) är 99, vilket nästan är 100. Genom att förlänga bråket med 3, får vi då bråket: \(78/99 ≈ 78/100\)

Detta ligger mycket nära svarsalternativ C, 80 procent.

Svar: C

Identifiera kolumnen för tilläggspension, och raderna för halvt respektive en fjärdedels uttag, för respektive kön. Markera dessa värden i tabellen: Det går att räkna exakt utan att det tar alltför lång tid, men genom att svarsalternativen ligger långt ifrån varandra, kan vi nöja oss med uppskattningar, vilka ger oss ett intervall svaret måste ligga inom. 

Halvt uttag: Skillnaden mellan män och kvinnor är 1800 - 1631. Det är större än 100, men mindre än 200.

En fjärdedels uttag: Skillnaden mellan män och kvinnor är 867 - 685. Det är större än 100, men mindre än 200.

Detta ger oss en summa som är större än 200, och mindre än 400. Det enda svar som ligger inom detta intervall, är B (351 personer).

Svar: B

Markera kolumnen för inkomstpension och premiepension i diagrammet: 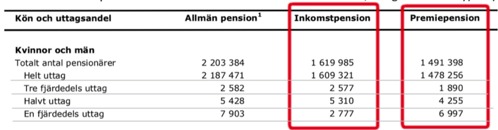 Ett förhållande mellan inkomstpension och premiepension på 2:5, innebär att antalet pensionärer med premiepension ska vara dubbelt så stort och lite till, som antalet med inkomstpension. Ett förhållande på 2:4 vore dubbelt så stort, medan vi söker förhållandet 2:5, vilket gör att premiepensionen ska vara ännu lite större än dubbelt så stor. 

För Helt uttag, Tre fjärdedels uttag och Halvt uttag är antalet med inkomstpension större än antalet med premiumpension. Det gör att endast alternativt En fjärdedels uttag kvarstår. 

För att dubbelkolla, kan vi kika på siffrorna. 2 777 personer med inkomstpension och 6 997 personer med premiumpension. 

2 777 är lite mindre än 3 000 personer, medan 6 997 kan avrundas till 70 00 utan att vi behöver ta någon hänsyn till hur den avrundningen påverkar svaret. 

Förhållandet 3 000 : 7 000 är detsamma som förhållandet 3:7, vilket är nästan 2:5. Förhållandet 3:7 är lite för jämnt (2:5 kan även förlängas till 3:7,5, för jämförelse). Men med tanke på att vi avrundade 2 777 uppåt lite grann för att få 3 000, stämmer förhållandet överens. 

Svar: D, En fjärdedels uttag

Markera respektive svarsalternativ i diagrammet:  

För att undvika slarvfel, bör vi först kontrollera att ordningen på svarsalternativen (som är stigande med ålder) är densamma som ordningen på staplarna i diagrammet (stapeln för lägst ålder ligger längst ned, och staplarna högre upp stiger med ålder). Det gör dem, så då kan vi börja utesluta alternativ. 

Staplarna för kvinnliga företagsledare (inom handel respektive företags- och konsulttjänster) har båda sin största stapel för 40–49 år. Därför kan vi utesluta alternativ B och C. 

Staplarna för män är jämnare, men genom att mäta höjden i diagrammet med linjal, går det snabbt att identifiera vilka staplar som ökar i storlek med ökande ålder. För män inom byggbranschen är stapeln för 50–59 år större än stapeln för 60+ år, och därför kvarstår endast alternativ A.

Svar: A, Företag inom Företags- och konsulttjänster med män som företagsledare

Den bransch där stapeln för kvinnor är högre än män är “Personliga och kulturella tjänster”. För att få ut totala antalet företag behöver vi summera stapeln för kvinnor ≈ 30 000 och män ≈ 20 000 och de blir tillsammans 50 000, dvs alternativ B.

Svar: B

Vi identifierar vilken stapel vi ska undersöka vilken åldersgrupp som utgör en åttondel.

De övre åldersgrupperna, 60- och 50-59 kan uteslutas direkt då de utgör ungefär en fjärdedel eller en tredjedel av stapeln. Vi undersöker den gråa delen av fältet, åldersgruppen 30-39. Vi mäter dess längd och måttar sedan hur många gånger den längden får plats i stapeln, så här representerat av blåa pilarna:
 
Den får plats 8 gånger, alltså utgör den en åttondel.

Svar: C

Vi använder skalan vi fått längst ner som motsvarar 50 km, vi behöver två sådana längder som ska utgöra radie. Sedan ritar vi en cirkel med den radien (2 st 50 km, röda pilar) och räknar antal städer, exklusive Stockholm. Se bilden nedan.

Vi har 6 städer inom cirkeln, Västerås, Torshälla, Eskilstuna, Strängnäs, Enköping och Uppsala. 

Svar:  A

Vi mäter diametern på cirklarna som Västerås (blå pil) och Örebro (röd pil), se bild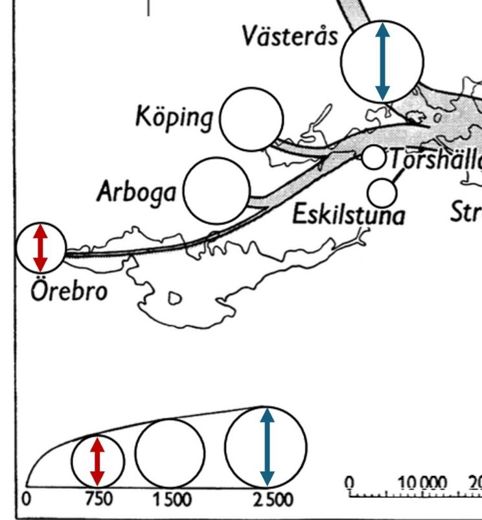

Vi får att skillnaden är 2500-750 = 1750 tunnor
Svar:  C

Bredden på det grå fältet som markerar transporter till Stockholm är 46 mm medan det som markerar transport vidare från Stockholm är 12 mm. Det som stannar i Stockholm motsvarar då 34 mm. 34 av 46 är en andel på 74 %. Dvs närmast 70%

Svar: C

Den 22 mars 2016 var antalet tranor ca 5 000 den 25:e var det 15000. Ökningen 10 000 tranor utgör en ökning på 200% av startvärdet 5 000.

Svar: B, 200 procent.

Den 26 mars 2010 var antalet tranor 2 500. Antalet 7 500 tranor uppnåddes den 30:e mars. Alltså 4 dagar senare. Se följande bild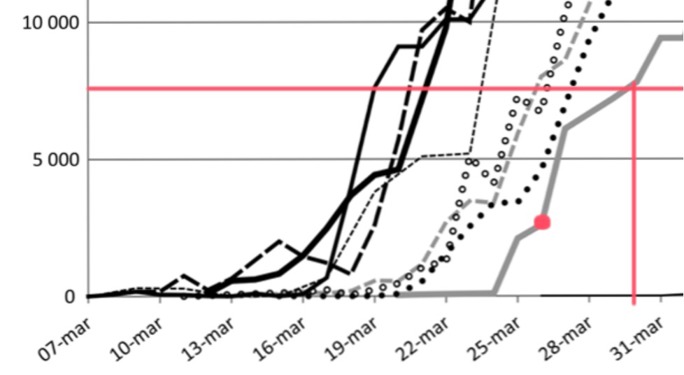

Svar: B

Dagen då antalet tranor var som störst, var den tredje april 2012. Då uppmättes antalet till 27 000 tranor. Den 3:e april 2009, tre år tidigare, var antalet tranor strax över 15 000.

Skillnaden i antal är 27 000 - 15 000 = 12 000, vilket stämmer väl överens med svarsalternativ D, 11 500.

Svar: D